[#] Sisällön pääryhmät --> Geometrian peruskäsitteet --> Determinantti [ 1 ]
ESITIEDOT:
KATSO MYÖS: [#] vektorialgebra
[#] Kansisivu
[#] Sisältö
[#] Hakemisto

Determinantti

Determinantin käsitteellä on sangen laaja käyttö lineaarialgebraksi ja matriisilaskennaksi kutsutuilla matematiikan osa-alueilla. Seuraavassa esitetään määrittelyt vain kaksi- ja kolmirivisille determinanteille, joita tarvitaan vektorialgebrassa. Kaksirivinen determinantti muodostuu neljästä 2 × 2-kaavioon järjestetystä luvusta (tai symbolista, joilla voidaan suorittaa laskutoimituksia; esimerkiksi vektoreista). Determinantti voidaan laskea, jolloin saadaan seuraava tulos:

| | || a11 a12|| | a21 a22| = a11a22 - a12a21.

Esimerkiksi:

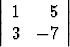|| 1 5 || || || 3 - 7 = 1 . (-7) - 5 . 3 = -22.

Vastaavasti kolmirivinen determinantti on 3 × 3-kokoinen kaavio, joka lasketaan seuraavasti:

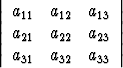| | || a11 a12 a13|| || a21 a22 a23|| | a31 a32 a33| = a11|| || || a22 a23 || a32 a33 - a12|| || ||a21 a23 || a31 a33 + a13|| || ||a21 a22 || a31 a32 .

Laskenta palautuu siis kaksirivisten determinanttien laskemiseen.

Esimerkiksi:

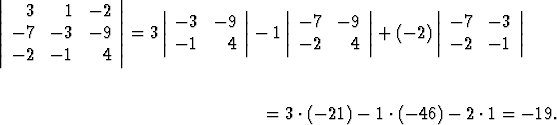
|| || | | | | | | | 3 1 - 2 | | -3 - 9 | | - 7 - 9 | | - 7 - 3 | ||- 7 - 3 - 9 ||= 3 || -1 4 || - 1|| - 2 4 ||+ (- 2)|| - 2 - 1 || |- 2 - 1 4 | = 3 .(- 21)- 1 .(- 46) - 2 .1 = - 19.

  [#] vektoritulon laskeminen
 [#] skalaarikolmitulo
 [#] vektori

Kivelä, M niinkuin matematiikka, versio 1.12