Sisällön pääryhmät Geometrian peruskäsitteet Vektorialgebra [ 1 2 3 4 5 ] ESITIEDOT:  vektori KATSO MYÖS:  determinantti

Kansisivu  Sisältö  Hakemisto

Vektoreiden yhteenlaskun ja skalaarilla kertomisen lisäksi vektoreiden välille voidaan määritellä myös kertolasku. Itse asiassa näitä on kaksi erilaista.

Seurauksena on, että vektoreilla voidaan laskea samaan tapaan kuin reaali- tai kompleksiluvuilla. Tällöin puhutaan vektorialgebrasta.

Tason tai avaruuden kahden vektorin skalaaritulo eli sisätulo eli pistetulo a ^. b määritellään asettamalla

a ^. b = |a||b| cos ,

missä on vektoreiden a ja b välinen kulma (0 < < ).

Vektorin skalaaritulo itsensä kanssa on sama kuin vektorin pituuden neliö, a ^. a = |a|², koska tällöin = 0 ja kosini siis on = 1.

Jos vektorit a ja b ovat toisiaan vastaan kohtisuoria, on niiden välisen kulman /2 kosini = 0 ja siis a ^. b = 0. Skalaaritulo voi olla = 0 myös sen takia, että jompikumpi (tai molemmat) vektoreista on nollavektori. Tapana on sanoa, että nollavektori on kohtisuorassa mitä tahansa vektoria vastaan, jolloin voidaan yksinkertaisesti kirjoittaa: a ^. b = 0, jos ja vain jos a ja b ovat kohtisuorat.

Koska kosinin itseisarvo on < 1, on |a ^. b| < |a||b|.

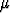Määritelmän pohjalta voidaan geometrisilla konstruktioilla osoittaa, että skalaaritulo on vaihdannainen ja noudattaa osittelulakeja. Skalaariset kertoimet voidaan kerätä yhteen: (a) ^. (b) = 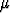(a ^. b). Tulon liitännäisyydestä ei sen sijaan voida puhua: Koska tulon arvo a ^. b on skalaari, ei sen skalaarituloa kolmannen vektorin kanssa voida muodostaa.

Jos tason vektorit on esitetty kantavektoreiden i ja j lineaariyhdistelyinä, saadaan skalaaritulolle yksinkertainen lauseke. Olkoon a = a_xi + a_yj ja b = b_xi + b_yj. Näiden skalaaritulo on em. laskulakien mukaan

a ^. b = a_xb_x + a_yb_y + a_zb_z.

vektori  yhteenlasku (vektorien)  skalaarilla kertominen (vektorien)  kosini  kulma (taso-)  pituus (vektorin)  nollavektori  vaihdannaisuus  osittelulaki  liitännäisyys  kantavektori  lineaariyhdistely

Kivelä, niinkuin matematiikka, versio 1.12