Sisällön pääryhmät Yhtälöt ja epäyhtälöt Itseisarvoyhtälöt [ 1 2 3 4 ] ESITIEDOT:  yhtälöt KATSO MYÖS:  polynomiyhtälöt

Kansisivu  Sisältö  Hakemisto

Saman yhtälön |x + 3| = |x² - 1| + 2x + 2 ratkaiseminen voidaan tehdä myös seuraavasti:

Korottamalla yhtälö puolittain toiseen potenssiin saadaan

x² + 6x + 9 = (x² - 1)² + (2x + 2)² + 2(2x + 2)|x² - 1|,

mikä voidaan sieventää muotoon

-x⁴ - x² - 2x + 4 = 2(2x + 2)|x² - 1|.

Jotta itseisarvomerkit saataisiin poistetuiksi, on korotettava uudelleen neliöön, jolloin sievennysten jälkeen saadaan kahdeksannen asteen yhtälö

x⁸ - 14x⁶ - 28x⁵ + 9x⁴ + 68x³ + 12x² - 48x = 0.

Tällä on juuret (ks. polynomiyhtälöt)

x₁ = -2,  x₂ = 0,  x₃₄ = 1,  x₅₆ = (3 ± ),  x₇₈ = (-3 ± i).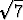

Kaksi viimeistä, x₇, x₈, eivät kompleksisina tule kysymykseen ja juuret x₅, x₆ eivät toteuta alkuperäistä yhtälöä, kuten sijoittamalla voidaan todeta. Ratkaisut ovat siis samat kuin tavan 1 antamat: x = -2, x = 0 ja x = 1.

sieventäminen (yhtälön)  yhtälö (polynomi-)

Kivelä, niinkuin matematiikka, versio 1.12