Sisällön pääryhmät Todennäköisyys Todennäköisyysjakaumat [ 1 2 3 4 5 ] ESITIEDOT:  todennäköisyyslaskenta,  määrätty integraali KATSO MYÖS:  tilastomatematiikka

Kansisivu  Sisältö  Hakemisto

Jatkuvista jakaumista tärkein on normaalijakauma. Sitä tarvitaan sekä monissa sovelluksissa että teoreettisissa tarkasteluissa kuvaamaan ilmiöitä, joissa keskialueen arvot ovat tietyllä tavalla todennäköisempiä kuin kummankin ääripään arvot.

Standardinormaalijakauman tiheysfunktio on

(x) = e^-x2/2, x .

Tämän kuvaajaa kutsutaan Gaussin kellokäyräksi.

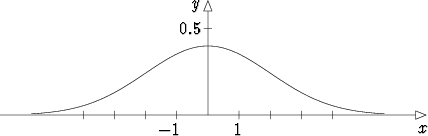
Standardinormaalijakauman kertymäfunktio on

(x) = e^-t2/2 dt,

missä integraalia ei voida laskea tavallisten alkeisfunktioiden avulla. Useat tietokoneohjelmat kuitenkin kykenevät laskemaan funktiolle (x) numeerisia arvoja. Näitä on myös taulukoituina.

Standardinormaalijakauman odotusarvo on 0 ja keskihajonta 1.

Normaalijakaumasta käytetään usein myös yleistä muotoa, jossa odotusarvo on = 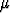ja keskihajonta = . Tiheysfunktio ja kertymäfunktio ovat tällöin

f(x)	= e-(x-)2/(22) =
F (x)	= e-(t-)2/(22) dt = .

Gauss  integraalifunktio  alkeisfunktio

Kivelä, niinkuin matematiikka, versio 1.12