![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Todennäköisyys
Todennäköisyys  Todennäköisyysjakaumat [
1 2 3 4 5 ]
Todennäköisyysjakaumat [
1 2 3 4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) todennäköisyyslaskenta,
todennäköisyyslaskenta, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali
määrätty integraali
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) tilastomatematiikka
tilastomatematiikka
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Todennäköisyys Todennäköisyys  Todennäköisyysjakaumat [
1 2 3 4 5 ] Todennäköisyysjakaumat [
1 2 3 4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) todennäköisyyslaskenta, todennäköisyyslaskenta, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) tilastomatematiikka tilastomatematiikka
|
|
Olkoon X diskreetti stokastinen muuttuja, joka saa erilliset arvot x1, x2, ..., xn. (Näitä voi olla myös ääretön määrä: xk, missä k saa arvoikseen kaikki luonnolliset luvut.)
Diskreetin stokastisen muuttujan jakauma, diskreetti jakauma, so. muuttujan saamiin arvoihin liittyvät todennäköisyydet voidaan määritellä antamalla pistetodennäköisyydet pk jokaiselle indeksille k:
P (X = xk) = pk.
Nämä ovat > 0 ja niiden summa on 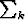 pk = 1. Pistetodennäköisyydet voidaan
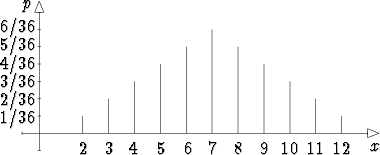
graafisesti esittää pystysuorien janojen avulla. Esimerkiksi kahta noppaa
heitettäessä pistelukujen summa on stokastinen muuttuja, joka saa arvot
2, 3, ..., 12. Näiden todennäköisyysjakauma ilmenee seuraavasta graafisesta
esityksestä:
pk = 1. Pistetodennäköisyydet voidaan
graafisesti esittää pystysuorien janojen avulla. Esimerkiksi kahta noppaa
heitettäessä pistelukujen summa on stokastinen muuttuja, joka saa arvot
2, 3, ..., 12. Näiden todennäköisyysjakauma ilmenee seuraavasta graafisesta
esityksestä:
Usein esiintyvä diskreetti jakauma on binomijakauma. Tämä kuvaa saman kokeen
toistamista, missä toistot ovat toisistaan riippumattomia ja kussakin toistossa
tuloksena on joko A tai tämän komplementtitapahtuma 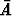 . Jos näiden
todennäköisyydet ovat P (A) = p ja P (
. Jos näiden
todennäköisyydet ovat P (A) = p ja P (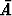 ) = 1 - p, niin toistettaessa koe n kertaa
saadaan tulos A täsmälleen k kertaa todennäköisyydellä
) = 1 - p, niin toistettaessa koe n kertaa
saadaan tulos A täsmälleen k kertaa todennäköisyydellä
pk =  pk(1 - p)n-k, k = 0, 1, ..., n.
pk(1 - p)n-k, k = 0, 1, ..., n.
Diskreettejä jakaumia on paljon muitakin.
![[#]](kuvat/msam10-c-4.gif) stokastinen muuttuja (diskreetti) stokastinen muuttuja (diskreetti)![[#]](kuvat/msam10-c-4.gif) todennäköisyys (funktio) todennäköisyys (funktio)![[#]](kuvat/msam10-c-4.gif) todennäköisyys
(funktio) todennäköisyys
(funktio)![[#]](kuvat/msam10-c-4.gif) summamerkintä summamerkintä![[#]](kuvat/msam10-c-4.gif) riippumattomuus (todennäköisyyslaskennassa) riippumattomuus (todennäköisyyslaskennassa)![[#]](kuvat/msam10-c-4.gif) komplementtitapahtuma komplementtitapahtuma |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12