![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Integraalifunktio [ 1 2 3 4
]
Integraalifunktio [ 1 2 3 4
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) derivaatta,
derivaatta, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt,
derivointisäännöt, ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden derivaatat
alkeisfunktioiden derivaatat
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) määrätty integraali,
määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa
integroimistekniikkaa
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Integraalifunktio [ 1 2 3 4
] Integraalifunktio [ 1 2 3 4
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) derivaatta, derivaatta, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt, derivointisäännöt, ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden derivaatat alkeisfunktioiden derivaatat
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) määrätty integraali, määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa integroimistekniikkaa
|
|
Reaalifunktion f integraalifunktioksi sanotaan jokaista funktiota, jonka derivaatta on f.
Integraalifunktio ei ole yksikäsitteinen. Jos F (x) on funktio, jonka derivaatta on f(x), myös jokaisen funktion F (x) + C, missä C on vakio, derivaatta on f(x). Saman funktion integraalifunktiot voivat siis erota toisistaan vakiolla. Toisaalta voidaan todistaa, että muunlaisia eroja ei voi olla.
Funktion f kaikkia integraalifunktioita merkitään
 f(x) dx.
f(x) dx.
Helposti derivoimalla tarkistettavia esimerkkejä ovat seuraavat:
 x2 dx x2 dx | =  x3 + C, x3 + C, |
 |x| dx |x| dx | =  x|x| + C, x|x| + C, |
 (1 + tan2x) dx (1 + tan2x) dx | = tan x + C, |
 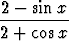 dx dx | =  arctan( arctan( tan(x/2)) + ln(2 + cos x) + C. tan(x/2)) + ln(2 + cos x) + C. |
Joukko integrointikaavoja saadaan suoraan alkeisfunktioiden derivointikaavoista. Hankalampia tapauksia varten tarvitaan erityisiä integrointitekniikkoja kuten sijoitusmenettelyä tai osittaisintegrointia. Kaikkia yksinkertaisiakaan funktioita ei kuitenkaan voida integroida alkeisfunktioiden avulla; esimerkkejä tällaisista ovat
ex2
,  ,
,  .
.
Summan derivoimiskaavan ja vakiokerrannaisen derivoimiskaavan perusteella saadaan
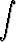 [f(x) + g(x)] dx = [f(x) + g(x)] dx =  f(x) dx + f(x) dx +  g(x) dx, g(x) dx, | ||||
 [cf(x)] dx = c [cf(x)] dx = c f(x) dx (c vakio), f(x) dx (c vakio), |
![[#]](kuvat/msam10-c-4.gif) funktio (reaali-) funktio (reaali-)![[#]](kuvat/msam10-c-4.gif) derivaatta derivaatta![[#]](kuvat/msam10-c-4.gif) derivointi (alkeisfunktioiden) derivointi (alkeisfunktioiden)![[#]](kuvat/msam10-c-4.gif) integrointi (sijoitus) integrointi (sijoitus)![[#]](kuvat/msam10-c-4.gif) integrointi (osittais-) integrointi (osittais-)![[#]](kuvat/msam10-c-4.gif) derivaatta (summan) derivaatta (summan)![[#]](kuvat/msam10-c-4.gif) derivaatta (vakiokerrannaisen) derivaatta (vakiokerrannaisen) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12