![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Alkeisfunktiot
Alkeisfunktiot  Arcus-funktiot [ 1 2 3
]
Arcus-funktiot [ 1 2 3
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) trigonometriset funktiot
trigonometriset funktiot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) trigonometrian kaavat
trigonometrian kaavat
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Alkeisfunktiot Alkeisfunktiot  Arcus-funktiot [ 1 2 3
] Arcus-funktiot [ 1 2 3
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) trigonometriset funktiot trigonometriset funktiot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) trigonometrian kaavat trigonometrian kaavat
|
|
Seuraavassa käsitellään vain arcus-funktioiden päähaaroja.
Käänteisfunktion yleisten ominaisuuksien mukaan on
| sin(arcsin y) = y, | arcsin(sin x) = x; |
| cos(arccos y) = y, | arccos(cos x) = x; |
| tan(arctan y) = y, | arctan(tan x) = x; |
| cot(arccot y) = y, | arccot(cot x) = x. |
Tämä edellyttää, että muuttuja x tai y on ao. funktion määrittelyjoukossa siten kuin edellä on esitetty.
Vasemmanpuoliset kaavat ovat sikäli ongelmattomampia, että jos muuttuja y
yleensä sijaitsee siten, että arcus-funktio on määritelty, niin kaava on oikea.
Oikeanpuolisissa kaavoissa muuttujan x on oltava rajoitetussa määrittelyjoukossa
eli päähaara-alueella — siis esimerkiksi sinin tapauksessa välillä [- /2,
/2,  /2] —
jotta kaava olisi voimassa.
/2] —
jotta kaava olisi voimassa.
Esimerkiksi arcsin(sin( /6)) =
/6)) =  /6, mutta jos x = 5
/6, mutta jos x = 5 /6, onkin laskettava
seuraavasti:
/6, onkin laskettava
seuraavasti:
arcsin(sin(5 /6)) = arcsin(sin(
/6)) = arcsin(sin( - 5
- 5 /6)) = arcsin(sin(
/6)) = arcsin(sin( /6)) =
/6)) =  /6.
/6.
Tässä on käytetty hyväksi sinin symmetriaa: sin x = sin( - x). Yhdistämällä
arcus-funktioita sopivasti saadaan funktioita, joiden kuvaajat saattavat näyttää
hieman yllättäviltäkin. Esimerkiksi:
- x). Yhdistämällä
arcus-funktioita sopivasti saadaan funktioita, joiden kuvaajat saattavat näyttää
hieman yllättäviltäkin. Esimerkiksi:
f(x) = arccos(sin x), g(x) = arctan x + arctan  .
.
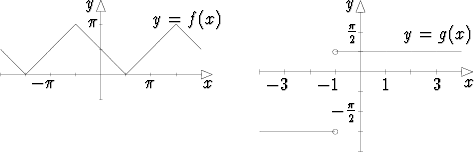
![[#]](kuvat/msam10-c-4.gif) käänteisfunktio käänteisfunktio![[#]](kuvat/msam10-c-4.gif) käänteisfunktio käänteisfunktio![[#]](kuvat/msam10-c-4.gif) määrittelyjoukko määrittelyjoukko![[#]](kuvat/msam10-c-4.gif) trigonometrinen funktio
(symmetria) trigonometrinen funktio
(symmetria) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12