Sisällön pääryhmät Funktio Reaalifunktiot [ 1 2 3 4 5 ] ESITIEDOT:  funktiokäsite KATSO MYÖS:  potenssi,  juuret,  polynomit,  rationaalifunktiot,  eksponenttifunktio,  logaritmifunktio,  trigonometriset funktiot,  arcus-funktiot,  hyperbelifunktiot,  area-funktiot

Kansisivu  Sisältö  Hakemisto

Tunnetun funktion f käänteisfunktio g voidaan usein löytää ratkaisemalla yhtälö y = f(x) muuttujan x suhteen. Jos ratkaisu on yksikäsitteinen tietyillä arvoilla y, saadaan tästä käänteisfunktion lauseke muodossa x = g(y).

Esimerkiksi funktio

f(x) =

on määritelty, kun x3. Käänteisfunktio saadaan ratkaisemalla x yhtälöstä y = f(x):

y = x = .

Ratkaisu on mahdollinen ja tulos yksikäsitteinen, jos y1. Käänteisfunktio on siis määritelty, kun sen argumentti on 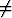1. Kun tavanomaiseen tapaan merkitään funktion argumenttia x, on käänteisfunktion lauseke

g(x) = , x1.

Vaikka käänteisfunktio olisi olemassa, ei sille välttämättä saada lauseketta edellä esitetyllä menettelyllä. Esimerkiksi funktion

f(x) =

tapauksessa jouduttaisiin ratkaisemaan viidennen asteen polynomiyhtälö x⁵ - yx² - y = 0, mikä ei ole juurilausekkeiden avulla mahdollista. Tästä huolimatta käänteisfunktio on olemassa, mikä voidaan päätellä osoittamalla funktio f derivaatan avulla aidosti kasvavaksi. Tällöin f on bijektio ja käänteisfunktio siis olemassa. Alkeisfunktioiden avulla muodostettua lauseketta sille ei kuitenkaan saada.

funktio  käänteisfunktio  käänteisfunktio  yhtälö  yhtälö (polynomi-)  juuri (murtopotenssi)  derivaatta  kasvava (funktio)  kasvava (funktio)  bijektio

Kivelä, niinkuin matematiikka, versio 1.12