[#] Sisällön pääryhmät --> Alkeisfunktiot --> Arcus-funktiot [ 1 2 3 ]
ESITIEDOT: [#] reaalifunktiot, [#] trigonometriset funktiot
KATSO MYÖS: [#] trigonometrian kaavat
[#] Kansisivu
[#] Sisältö
[#] Hakemisto

Arcus-funktioiden määritelmät

Trigonometriset funktiot eivät sellaisinaan ole bijektioita eikä niillä siis ole käänteisfunktioita. Jos funktioiden määrittelyjoukkoja kuitenkin sopivasti rajoitetaan, saadaan bijektiot. Neljän tärkeimmän funktion osalta on rajoitus tehtävä seuraavasti:

sin : [-p/2,  p/2]  -->  [-1,  1] ;
  
cos : [0,  p]  -->  [-1,  1] ;
  
tan : ] - p/2,  p/2[ -->  R ;
  
cot : ]0,  p[ -->  R .

Täten rajoitettuina funktiot ovat surjektioita, ts. jokainen maalijoukon piste on myös jonkin määrittelyjoukon pisteen kuva. Funktioista sin ja tan ovat aidosti kasvavia, cos ja cot aidosti väheneviä; jokaiselle maalijoukon pisteelle kuvautuu siis täsmälleen yksi lähtöjoukon piste, jolloin funktiot ovat todellakin bijektioita.

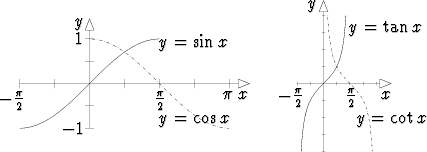
Tällöin funktioilla on käänteisfunktiot. Näitä kutsutaan arcus-funktioiksi eli syklometrisiksi funktioiksi ja merkitään

arcsin : [-1,  1]  -->  [-p/2,  p/2] ;
  
arccos : [-1,  1]  -->  [0,  p] ;
  
arctan : R  --> ] - p/2,  p/2[ ;
  
arccot : R  --> ]0,  p[ .

Funktioiden nimet luetaan arkussini, arkuskosini, jne.

Sana arcus tarkoittaa kaarta. Radiaaneja käytettäessä kaaren pituus on sama kuin vastaava yksikköympyrän keskuskulma. Merkintä a = arcsin y on siis ymmärrettävä siten, että kyseessä on sinin arvoa y vastaava kaari eli kulma a. Muut arcus-funktioiden nimet vastaavaan tapaan.

  [#] bijektio
 [#] käänteisfunktio
 [#] käänteisfunktio
 [#] määrittelyjoukko
 [#] väli (reaaliakselin)
 [#] surjektio
 [#] maalijoukko
 [#] kasvava (funktio)
 [#] kasvava (funktio)
 [#] vähenevä (funktio)
 [#] vähenevä (funktio)
 [#] lähtöjoukko
 [#] radiaani
 [#] keskuskulma

Kivelä, M niinkuin matematiikka, versio 1.12