![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Integroimistekniikkaa [ 1 2 3
4 5 ]
Integroimistekniikkaa [ 1 2 3
4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) integraalifunktio,
integraalifunktio, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali,
määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt
derivointisäännöt
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Integroimistekniikkaa [ 1 2 3
4 5 ] Integroimistekniikkaa [ 1 2 3
4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) integraalifunktio, integraalifunktio, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali, määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt derivointisäännöt
KATSO MYÖS: |
|
1) Integraali
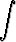 x2ex dx
x2ex dx
voidaan laskea kahdella peräkkäisellä osittaisintegroinnilla. Ensimmäinen antaa seuraavaa:
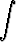
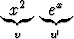 dx =
dx = 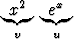 -
- 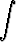
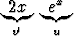 dx.
dx.
Kun saatuun integraaliin sovelletaan uudelleen osittaisintegrointia saadaan kaikkiaan
x2ex - 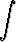 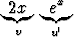 dx dx | = | x2ex - 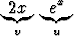 + + 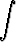 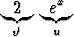 dx dx | ||
| = | x2ex - 2xex + 2ex + C = ex(x2 - 2x + 2) + C. |
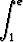 ln x dx ln x dx | = | 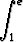 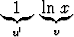 dx = dx = 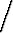 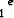 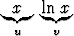 - - 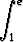 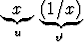 dx dx | ||
| = | e - 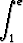 dx = e - (e - 1) = 1. dx = e - (e - 1) = 1. |
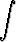
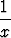 dx =
dx = 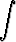 1 .
1 . 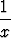 dx = x .
dx = x . 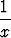 +
+ 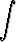 x .
x . 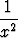 = 1 +
= 1 + 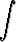
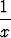 dx.
dx.
Siis
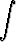
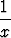 dx = 1 +
dx = 1 + 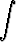
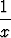 dx,
dx,
mistä seuraa 0 = 1, kun integraalit supistetaan pois.
![[#]](kuvat/msam10-c-4.gif) integraalifunktio integraalifunktio![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali![[#]](kuvat/msam10-c-4.gif) logaritmifunktio logaritmifunktio |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12