[#] Sisällön pääryhmät --> Integraali --> Integroimistekniikkaa [ 1 2 3 4 5 ]
ESITIEDOT: [#] integraalifunktio, [#] määrätty integraali, [#] derivointisäännöt
KATSO MYÖS:
[#] Kansisivu
[#] Sisältö
[#] Hakemisto

Esimerkkejä sijoitusmenettelystä I

1) Integraali

integral --dx---- 2x2 + 1

voidaan palauttaa arctan-funktion derivaatan integroimiseen sijoittamalla t = 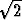V~ -- 2 x, jolloin dt = V~ -- 2 dx:

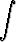integral dx --2----- 2x + 1 = integral V~ d2t 2----- t + 1 = 1 V~ -- 2 integral dt 2----- t + 1 = 1 V~ -- 2 arctan t + C
      = 1 V~ -- 2 arctan( V~ -- 2 x) + C.

Lopuksi on siis palattu takaisin alkuperäiseen muuttujaan x. 2) R-säteisen puoliympyrän ala voidaan laskea integraalista

integral R - R V~ -------- R2 - x2 dx.

Tämä saadaan lasketuksi sijoittamalla x = R sin t, jolloin dx = R cos t dt. Yläraja muunnetaan ratkaisemalla yhtälö R = R sin t; tällä on useita ratkaisuja, mutta luontevinta on valita arcsin-funktion päähaaran mukainen arvo t = p/2. Alarajan muuntaminen antaa vastaavasti t = -p/2. Tulosta voidaan sieventää trigonometrian kaavoilla:

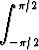integral R -RV ~ -2----2- R - x dx = integral p/2 - p/2 V~ --2-----2---2- R - R sin t R cos t dt
= integral p/2 -p/2R2 cos2t dt = R2 integral p/2 - p/21 2(1 + cos 2t) dt
= R2/p/2 -p/21 2(t + 1 2 sin 2t) = 1 2pR2.

  [#] integraalifunktio
 [#] arcus-funktio
 [#] integrointi (kaavat)
 [#] integrointi (kaavat)
 [#] ympyrä (esimerkki)
 [#] ympyrä
 [#] ympyrä (ala)
 [#] määrätty integraali
 [#] pinta-ala (integroimalla)
 [#] trigonometria (johdannaiskaavat)

Kivelä, M niinkuin matematiikka, versio 1.12