Sisällön pääryhmät Kulma, kolmio, monikulmio ja -tahokas Kulma [ 1 2 3 4 ] ESITIEDOT:  piste,  suora,  taso,  ympyrä,  pallo KATSO MYÖS:  vektorialgebra

Kansisivu  Sisältö  Hakemisto

Kahden toisiaan leikkaavan tason välistä kulmaa — yleensä pienempää kahdesta mahdollisesta — kutsutaan tasojen diedrikulmaksi.

Sen suuruutta mitataan asettamalla tasojen leikkaussuoraa vastaan kohtisuora taso. Alkuperäiset tasot leikkaavat tätä pitkin kahta suoraa ja näiden välisen (pienemmän) tasokulman suuruus on diedrikulman suuruus.

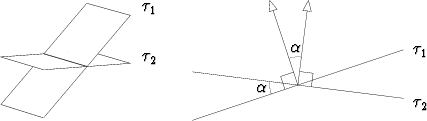
Diedrikulman suuruus voidaan helposti laskea määrittämällä ensin tasojen normaalivektorit. Näiden välinen kulma on joko pienempi tai isompi diedrikulma siitä riippuen, kummalle puolen tasoja normaalivektorit osoittavat.

Esimerkiksi tasojen x + 2y + 3z = 4 ja 4x - 3y + 2z = -1 normaalivektorit saadaan muuttujien kertoimista:

n₁ = i + 2j + 3k, n₂ = 4i - 3j + 2k.

Skalaaritulon avulla voidaan laskea näiden välinen kulma :

cos = =

ja siis 1.37 rad 78.5^o.

taso  suora  normaalivektori (tason)  taso (yhtälö)  skalaaritulo

Kivelä, niinkuin matematiikka, versio 1.12