Sisällön pääryhmät Kulma, kolmio, monikulmio ja -tahokas Kulma [ 1 2 3 4 ] ESITIEDOT:  piste,  suora,  taso,  ympyrä,  pallo KATSO MYÖS:  vektorialgebra

Kansisivu  Sisältö  Hakemisto

Kiinnitetään jokin kolmiulotteisen avaruuden piste K kulman kärjeksi. Olkoon avaruudessa lisäksi annettuna riittävässä määrin säännöllinen sulkeutuva käyrä (esimerkiksi ympyrä), joka ei kulje pisteen K kautta. Asetetaan pisteestä K alkavat puolisuorat, jotka kulkevat käyrän jonkin pisteen kautta. Puolisuorat muodostavat pinnan, jota kutsutaan yleiseksi kartiopinnaksi. Tämä rajaa avaruuden kahteen — pienempään ja isompaan — avaruuskulmaan samaan tapaan kuin tasokulman kyljet rajaavat kaksi tasokulmaa.

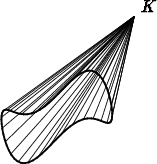
Avaruuskulman suuruus määritellään asettamalla pallo siten, että sen keskipisteenä on kulman kärki. Kulman suuruus on pallon pinnasta kulman sisään (sen aukeamaan) jäävän osan pinta-alan suhde pallon säteen neliöön. Yksikköä kutsutaan nimellä steradiaani.

Täyden avaruuskulman suuruus on pallon pinta-ala jaettuna pallon säteen neliöllä, ts. 4 steradiaania.

Olkoon esimerkkinä avaruuskulma, jonka kärkenä on origo ja em. sulkeutuvana käyränä pisteitä (1, 0, 0), (0, 1, 0), (0, 0, 1) yhdistävät kolmion sivut. Avaruuskulmaa rajaavat puolisuorat sijaitsevat tällöin koordinaattitasoissa. Pienempi avaruuskulma muodostuu siitä avaruuden kahdeksanneksesta, jonka pisteiden koordinaatit ovat > 0. Suuruus on /2 steradiaania.

käyrä (avaruus-)  kartiopinta  kartiopinta  pallo  pallo (ala)  koordinaatisto (xyz-)  koordinaattitaso

Kivelä, niinkuin matematiikka, versio 1.12