Sisällön pääryhmät Lukujonon ja funktion raja-arvo Lukujonot [ 1 2 3 ] ESITIEDOT:  funktiokäsite KATSO MYÖS:  summa ja tulo,  lukujonon raja-arvo,  sarjat

Kansisivu  Sisältö  Hakemisto

Reaalisella lukujonolla tarkoitetaan peräkkäin lueteltuja reaalilukuja:

a₁,  a₂,  a₃, ... .

Vastaavasti puhutaan kompleksisesta lukujonosta, jos luvut a_k ovat kompleksilukuja. Yleensä ajatellaan, että lukuja on jonossa äärettömän paljon. Lukuja kutsutaan myös jonon termeiksi.

Esimerkiksi

1,  2,  4,  8,  16,  32,  64,  ... ja 1,  i,  -1,  -i,  1,  i,  -1,  -i,  ...

ovat lukujonoja. Edellinen on reaalinen jono, joka muodostuu luvun 2 potensseista, jälkimmäinen imaginaariyksikön i potensseista muodostuva kompleksinen jono.

Itse asiassa lukujono on funktio luonnollisten lukujen joukosta reaali- tai kompleksilukujen joukkoon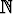, F : tai F : 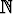. Funktion arvoja on vain tapana merkitä siten, että argumentti esitetäänkin alaindeksinä: F (1) = a₁, F (2) = a₂, yleisesti F (k) = a_k. Kakkosen potenssit käsittävässä lukujonossa on siis kyse funktiosta F (k) = 2^k-1.

Indeksoinnin ei välttämättä tarvitse alkaa luvusta 1, vaan yleensä jostakin lausekkeen kannalta luonnollisesta aloitusarvosta. Funktion F lähtöjoukko voi siis olla luonnollisten lukujen joukko täydennettynä tai supistettuna joillakin arvoilla. Esimerkiksi kakkosen potenssien muodostama jono voidaan aivan hyvin esittää myös muodossa F (k) = a_k = 2^k, k = 0, 1, 2, 3, ... . Toisena esimerkkinä olkoon a_k = 1/ ln k, k = 2, 3, 4, 5, ... .

reaaliluku  kompleksiluku  potenssi (kokonaisluku-)  imaginaariyksikkö  funktio  luonnollinen luku

Kivelä, niinkuin matematiikka, versio 1.12