Sisällön pääryhmät Kulma, kolmio, monikulmio ja -tahokas Monitahokkaat [ 1 2 3 4 ] ESITIEDOT:  monikulmiot,  taso KATSO MYÖS:  geometriset probleemat

Kansisivu  Sisältö  Hakemisto

Monitahokkaaksi kutsutaan kolmiulotteisen avaruuden kappaletta, jota rajaavat tasopinnat. Tasopinnat ovat monitahokkaan tahkot; nämä leikkaavat toisensa pitkin särmiä, joiden päätepisteet ovat monitahokkaan kärkiä.

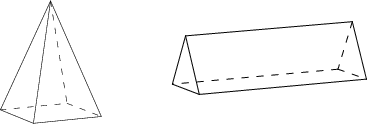
Jos monitahokkaassa ei ole aukkoja yllä olevan viimeisen esimerkin tapaan (täsmällisemmin sanottuna jos monitahokas on yhdesti yhtenäinen), on voimassa Eulerin yhtälö, jonka tosin jo Descartes tunsi:

f - e + v = 2,

missä f on monitahokkaan tahkojen lukumäärä, e särmien lukumäärä ja v kärkien lukumäärä. (Symbolit ovat englannista peräisin: face, edge, vertex.)

Jos monitahokkaassa on yksi tai useampia aukkoja, riippuu kaavan oikea puoli aukkojen lukumäärästä. Esimerkiksi yksiaukkoisessa tapauksessa on f - e + v = 0.

Euler  Descartes

Kivelä, niinkuin matematiikka, versio 1.12