[#] Sisällön pääryhmät --> Kulma, kolmio, monikulmio ja -tahokas --> Monitahokkaat [ 1 2 3 4 ]
ESITIEDOT: [#] monikulmiot, [#] taso
KATSO MYÖS: [#] geometriset probleemat
[#] Kansisivu
[#] Sisältö
[#] Hakemisto

Säännölliset monitahokkaat

Monitahokasta sanotaan säännölliseksi, jos sen kaikki tahkot ovat samanlaisia säännöllisiä monikulmioita ja kaikki kärjet samanlaisia.

Jo antiikin kreikkalaiset tiesivät, että säännöllisiä monitahokkaita on vain viisi: tetraedri, heksaedri eli kuutio, oktaedri, dodekaedri ja ikosaedri.

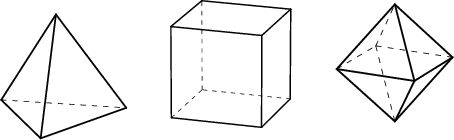
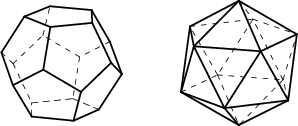
Näiden kärkien, särmien ja tahkojen määrät ovat seuraavat:

kärjet särmät tahkot
tetraedri 4 6 4
heksaedri 8 12 6
oktaedri 6 12 8
dodekaedri 20 30 12
ikosaedri 12 30 20

Yhdistämällä säännöllisen monitahokkaan sivutahkojen keskipisteet saadaan tämän sisään toinen säännöllinen monitahokas: Tetraedrin tapauksessa tetraedri, kuution sisään oktaedri ja oktaedrin sisään kuutio, dodekaedrin sisään ikosaedri ja ikosaedrin dodekaedri. Tämä on pääteltävissä edellä olevan taulukon symmetrioistakin.

  [#] monikulmio

Kivelä, M niinkuin matematiikka, versio 1.12