Sisällön pääryhmät Kulma, kolmio, monikulmio ja -tahokas Monitahokkaat [ 1 2 3 4 ] ESITIEDOT:  monikulmiot,  taso KATSO MYÖS:  geometriset probleemat

Kansisivu  Sisältö  Hakemisto

Jokaisesta säännöllisestä monitahokkaasta voidaan muodostaa uusi monitahokas seuraavalla tavalla: Jokaisen sivutahkon päälle asetetaan keskenään samanlaiset pyramidit, joiden pohjina sivutahkot ovat. Pyramidien korkeus valitaan siten, että kahden vierekkäisen pyramidin huiput ja niiden yhteisen pohjasärmän päätepisteet ovat samassa tasossa; näiden neljän pisteen määräämästä nelikulmiosta tulee uuden kappaleen sivutahko.

Tetraedrin tapauksessa tällöin syntyy kuutio. Kuutiosta ja oktaedrista saadaan monitahokas, jota kutsutaan rombidodekaedriksi (rombi = neljäkäs, vinoneliö). Dodekaedrista ja ikosaedrista syntyy sama 30-tahokas.

Rombidodekaedri ja em. 30-tahokas eivät ole säännöllisiä monitahokkaita, vaikka niistä onkin löydettävissä monia symmetrioita.

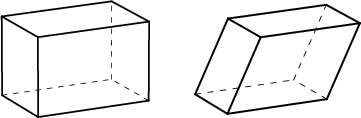
Yksinkertaisempia symmetrisiä, mutta ei säännöllisiä monitahokkaita ovat suorakulmainen särmiö, jonka kaikki sivutahkot ovat suorakulmioita (yhteensä kuusi), ja suuntaissärmiö eli paralleeliepipedi, jonka sivutahkot ovat suunnikkaita.

pyramidi  vinoneliö  särmiö (suorakulmainen)  särmiö (suuntais-)  särmiö (tilavuus)  suunnikas

Kivelä, niinkuin matematiikka, versio 1.12