Sisällön pääryhmät Luvut Luku [ 1 2 3 4 ] ESITIEDOT: KATSO MYÖS:  reaaliluvut

Kansisivu  Sisältö  Hakemisto

Alkeelliset menetelmät :n arvon laskemiseen perustuvat ympyrän sisään ja ympäri piirrettyjen monikulmioiden piirien laskemiseen. Jos ympyrän säde on = 1 ja ympyrän sisään piirretyn 2^k-kulmion sivun pituus s_k, saadaan 2^k+1-kulmion sivun pituudelle s_k+1 palautuskaava

s =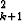

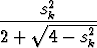
Pythagoraan lausetta ja yksinkertaista algebraa käyttäen.

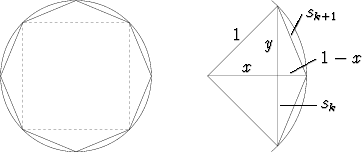
Kun lisäksi otetaan huomioon, että s₂ = 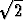, lukuja s₂,  s₃,  s₄,  ... voidaan laskea miten pitkälle tahansa. Koska s_k on 2^k-kulmion sivu ja 2^k-kulmion piiri ilmeisestikin lähestyy ympyrän kehän pituutta k:n kasvaessa, on

lim_k2^k-1s_k = .

Alalikiarvoja :lle saadaan siis luvuista 2^k-1s_k.

Vastaavasti saadaan ylälikiarvoja ympyrän ympäri piirretyistä 2^k-kulmioista.

monikulmio  Pythagoraan lause  raja-arvo (lukujonon)

Kivelä, niinkuin matematiikka, versio 1.12