Sisällön pääryhmät Integraali Integraalifunktio [ 1 2 3 4 ] ESITIEDOT:  derivaatta,  derivointisäännöt,  alkeisfunktioiden derivaatat KATSO MYÖS:  määrätty integraali,  integroimistekniikkaa

Kansisivu  Sisältö  Hakemisto

Alkeisfunktioiden derivointikaavoista saadaan suoraan seuraavat integrointikaavat tavallisimmille alkeisfunktioille:

x dx	= x+1 + C, ,  - 1,
dx	= ln |x| + C,
ex dx	= ex + C,
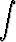sin x dx	= - cos x + C,
cos x dx	= sin x + C,
sinh x dx	= cosh x + C,
cosh x dx	= sinh x + C.

Huomattakoon kaava 1/x dx = ln |x| + C, missä logaritmin sisällä on itseisarvomerkit. Jos x > 0, tämä seuraa logaritmin derivoimiskaavasta. Jos x < 0, on integraalifunktio ln(-x), koska tämän derivaatta yhdistetyn funktion derivoimissäännön mukaisesti on 1/x. Itseisarvomerkit ovat usein oleelliset, koska integroitava funktio 1/x on määritelty myös argumentin negatiivisilla arvoilla, mutta ln x ei (reaalisena).

derivointi (alkeisfunktioiden)  alkeisfunktio  logaritmifunktio  derivaatta (yhdistetyn funktion)

Kivelä, niinkuin matematiikka, versio 1.12