![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Integraalifunktio [ 1 2 3 4
]
Integraalifunktio [ 1 2 3 4
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) derivaatta,
derivaatta, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt,
derivointisäännöt, ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden derivaatat
alkeisfunktioiden derivaatat
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) määrätty integraali,
määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa
integroimistekniikkaa
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Integraalifunktio [ 1 2 3 4
] Integraalifunktio [ 1 2 3 4
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) derivaatta, derivaatta, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt, derivointisäännöt, ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden derivaatat alkeisfunktioiden derivaatat
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) määrätty integraali, määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa integroimistekniikkaa
|
|
Koska integraalifunktio on derivoituva, se on myös jatkuva. Tähän ominaisuuteen on kiinnitettävä erityistä huomiota seuraavantyyppisissä tilanteissa.
Yhdistetyn funktion derivoimissääntöä käyttäen voidaan todeta, että funktion arctan(1/x) derivaatta on f(x) = -1/(1 + x2). Funktio arctan(1/x) ei kuitenkaan kelpaa integraalifunktioksi, koska se ei ole jatkuva origossa:
limx 0+ arctan(1/x) =
0+ arctan(1/x) = 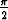 , limx
, limx 0- arctan(1/x) = -
0- arctan(1/x) = -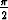 .
.
Määritelläänpä arvo origossa siis miten tahansa, funktiosta ei saada jatkuvaa.
Funktio
F (x) = 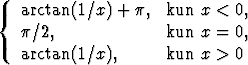
sen sijaan on origossa jatkuva ja myös derivoituva; erotusosamäärän raja-arvoa tarkastelemalla nähdään derivaataksi F '(0) = -1 = f(0). Funktion f(x) = -1/(1 + x2) kaikki integraalifunktiot ovat siten esitettävissä muodossa F (x) + C.
Jos toisaalta integroitavan funktion määrittelyalue jakautuu kahteen (tai useampaan) osaan esimerkiksi siten, että funktio ei jossakin pisteessä ole määritelty, voidaan integraalifunktio muodostaa kussakin osa-alueessa muista täysin riippumattomasti.
Esimerkiksi origo jakaa funktion f(x) = 1/x määritelyalueen kahteen osaan. Integraalifunktioksi voidaan tällöin aivan hyvin valita
F (x) = 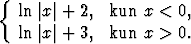
![[#]](kuvat/msam10-c-4.gif) derivoituvuus derivoituvuus![[#]](kuvat/msam10-c-4.gif) jatkuvuus jatkuvuus![[#]](kuvat/msam10-c-4.gif) derivaatta (yhdistetyn funktion) derivaatta (yhdistetyn funktion)![[#]](kuvat/msam10-c-4.gif) arcus-funktio arcus-funktio![[#]](kuvat/msam10-c-4.gif) derivaatta derivaatta![[#]](kuvat/msam10-c-4.gif) raja-arvo (toispuolinen) raja-arvo (toispuolinen)![[#]](kuvat/msam10-c-4.gif) erotusosamäärä erotusosamäärä![[#]](kuvat/msam10-c-4.gif) raja-arvo (funktion) raja-arvo (funktion) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12