Sisällön pääryhmät Derivaatta Maksimit ja minimit [ 1 2 3 4 5 ] ESITIEDOT:  reaalifunktiot,  derivaatta KATSO MYÖS:  funktion jatkuvuus,  derivointisäännöt,  alkeisfunktioiden derivaatat

Kansisivu  Sisältö  Hakemisto

Kolmion ABC sivulla AB sijaitsee piste P ja sivulla AC piste Q. Jana P Q jakaa kolmion kahteen yhtä suureen osaan. On etsittävä janan P Q pituuden suurin ja pienin arvo.

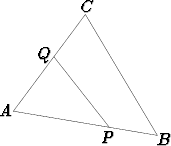
Olkoon kärjessä A sijaitseva kolmion kulma ja merkitään sivujen pituuksia b = |AB|, c = |AC|, x = |AP |, y = |AQ|. Koska kolmion AP Q ala on puolet kolmion ABC alasta, saadaan ehto xy sin = bc sin , mistä seuraa y = .

Probleemassa voidaan ottaa muuttujaksi x, jolle ehdoista 0 < x < b ja 0 < y < c saadaan rajoitukset b/2 < x < b.

Tutkittavaksi funktioksi on yksinkertaisinta ottaa janan P Q pituuden neliö, joka kosinilauseen mukaan on

s² = f(x) = x² + y² - 2xy cos = x² + - bc cos .

Funktio on tarkasteluvälillä derivoituva, joten riittää tutkia derivaatan nollakohdat ja välin päätepisteet. Derivaatan f'(x) = 2x - ainoa positiivinen nollakohta on x₀ = .

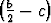Funktion arvot derivaatan nollakohdassa ja välin päätepisteissä ovat f(x₀) = bc - bc cos , f() = + c² - bc cos , f(b) = b² + - bc cos . Näistä arvoista ensimmäinen on pienin, sillä f() - f(x₀) = ² > 0, f(b) - f(x₀) = 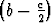² > 0.

Ei ole kuitenkaan selvää, että x₀ sijaitsee tarkasteluvälillä; tämä riippuu sivujen pituuksien b ja c suhteesta. Ehdosta b/2 < x₀ < b seuraa nimittäin b/2 < c < 2b; jos tämä ehto on täytetty, antaa x₀ minimin ja maksimi saadaan jommassakummassa päätepisteessä (riippuen sivujen pituuksien b ja c suhteesta). Jos ehto ei ole täytetty, ei derivaatalla ole lainkaan nollakohtia tarkasteluvälillä ja toinen päätepiste antaa maksimin, toinen minimin.

kolmio  kolmio (ala)  trigonometrinen funktio (suorakulmaisessa kolmiossa)  kosinilause  derivaatta  derivoituvuus  derivointi (alkeisfunktioiden)

Kivelä, niinkuin matematiikka, versio 1.12