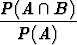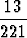Ehdollinen todennäköisyys
Tiettyyn ilmiöön liittyvän todennäköisyysfunktion P määrittämisen ohjenuorana
voidaan todennäköisyyden frekvenssitulkinnan mukaisesti pitää tilastollisia
kokeita. Haluttaessa määrittää todennäköisyys tapahtumalle B, kun tapahtuma A
on sattunut, on luonnollista suorittaa koesarja ja laskea tapaukset, joissa sattuu A
ja joissa sattuu sekä A että B. Jos näiden lukumäärät ovat n(A) ja n(A 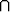 B),
todennäköisyyttä approksimoi suhde
B),
todennäköisyyttä approksimoi suhde
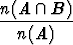 =
= 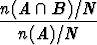 ,
,
missä N tarkoittaa sarjan kokeiden kokonaismäärää. Lausekkeen oikean puolen
voidaan tulkita approksimoivan tapahtumien A 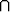 B ja A todennäköisyyksien
suhdetta P (A
B ja A todennäköisyyksien
suhdetta P (A 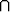 B)/P (A).
B)/P (A).
Ehdollinen todennäköisyys P (B|A) tapahtumalle B, kun tapahtuma A on
sattunut, määritellään tämän johdosta asettamalla
P (B|A) = 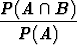 .
.
Esimerkkinä olkoon seuraava:
Hyvin sekoitetusta korttipakasta vedetään peräkkäin kaksi korttia. Ensimmäinen
osoittautuu ässäksi. Millä todennäköisyydellä toinenkin on ässä?
Kahden kortin variaatioita on 52 . 51 = 2652 kappaletta. On luonnollista pitää
näitä yhtä todennäköisinä, jolloin jokaisen todennäköisyys on 1/2652.
Tarkoittakoon A tapahtumaa ’ensimmäinen kortti on ässä, toinen mikä tahansa’
sekä B tapahtumaa ’toinen kortti on ässä, ensimmäinen mikä tahansa’.
Tapahtumia A ja A 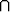 B vastaavien korttiparien lukumäärät ovat 4 . 51 = 204 ja
4 . 3 = 12, jolloin vastaavat todennäköisyydet ovat
B vastaavien korttiparien lukumäärät ovat 4 . 51 = 204 ja
4 . 3 = 12, jolloin vastaavat todennäköisyydet ovat
P (A) = 204 .  =
= 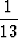 ja P (A
ja P (A 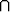 B) = 12 .
B) = 12 .  =
=  .
.
Kysytty ehdollinen todennäköisyys on tällöin
P (B|A) = 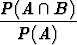 =
= 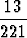 =
= 
 0.059.
0.059.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Todennäköisyys
Todennäköisyys  Todennäköisyyslaskenta [
1 2 3 4 5 6 7 ]
Todennäköisyyslaskenta [
1 2 3 4 5 6 7 ]
![[#]](kuvat/msam10-c-4.gif) joukko-oppi,
joukko-oppi, ![[#]](kuvat/msam10-c-4.gif) lukumäärän laskeminen,
lukumäärän laskeminen, ![[#]](kuvat/msam10-c-4.gif) funktiokäsite
funktiokäsite
![[#]](kuvat/msam10-c-4.gif) tilastomatematiikka,
tilastomatematiikka, ![[#]](kuvat/msam10-c-4.gif) todennäköisyysjakaumat
todennäköisyysjakaumat
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto
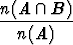
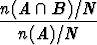
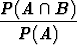

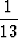 ja
ja