Sisällön pääryhmät Geometrian peruskäsitteet Vektorialgebra [ 1 2 3 4 5 ] ESITIEDOT:  vektori KATSO MYÖS:  determinantti

Kansisivu  Sisältö  Hakemisto

Vektoritulo eli ristitulo voidaan määritellä vain avaruuden vektoreille. Sitä merkitään a × b ja se määritellään seuraavilla ehdoilla:

• Ristitulovektorin pituus on |a×b| = |a||b| sin , missä on vektoreiden a ja b välinen kulma (0 < < ).
• Ristitulovektorin suunta määräytyy siten, että se on kohtisuorassa vektoreita a ja b vastaan; kahdesta mahdollisuudesta valitaan se, joka tekee vektorikolmikosta a, b, a × b oikeakätisen (so. kyseiset kolme vektoria suhtautuvat toisiinsa kuten oikean käden peukalo, etusormi ja keskisormi ojennettuina).
• Jos jompikumpi vektoreista a ja b on nollavektori, myös niiden ristitulo on nollavektori.

a × (b + c) = a × b + a × c (a + b) × c = a × c + b × c.

Skalaariset kertoimet voidaan myös kerätä yhteen:

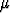(a) × (b) = 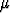(a × b).

Vaihdannainen tai liitännäinen ei vektoritulo sen sijaan ole. Tekijöiden järjestystä vaihdettaessa muuttuu merkki: a × b = -b × a. Esimerkiksi on (i × j) × j = k × j = -i ja i × (j × j) = i × o = o eikä liitännäisyys siis päde.

Vektorin vektoritulo itsensä kanssa on nollavektori: a × a = o. Tällöin nimittäin vektoreiden välinen kulma on = 0, jolloin tulovektorin pituus on = 0.

vektori  pituus (vektorin)  kulma (taso-)  koordinaatisto (oikeakätinen)  nollavektori  osittelulaki  vaihdannaisuus  liitännäisyys

Kivelä, niinkuin matematiikka, versio 1.12