Sisällön pääryhmät Geometrian peruskäsitteet Vektorialgebra [ 1 2 3 4 5 ] ESITIEDOT:  vektori KATSO MYÖS:  determinantti

Kansisivu  Sisältö  Hakemisto

Vektorin b skalaarikomponentti vektorin a suunnalle on

|b| cos = = a^0 . b.

Tämä voi myös olla negatiivinen, jos vektoreiden välinen kulma on > /2.

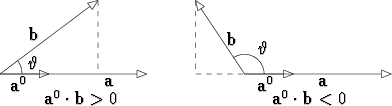
Vastaavasti saadaan vektorin b vektorikomponentti vektorin a suunnalle liittämällä skalaarikomponenttiin suunta:

|b| cos  a⁰ =  a = (a^0 . b) a⁰.

Vektorikomponentin suunta on siis joko vektorin a suunta tai sille vastakkainen suunta riippuen skalaaritulon a ^. b merkistä, ts. siitä, onko vektori b pikemminkin saman- vai vastakkaissuuntainen kuin a.

Jos vektori on esitetty lineaariyhdistelynä kantavektoreista, siis b = b_xi + b_yj + b_zk, on

b ^. i = b_xi ^. i + b_yj ^. i + b_zk ^. i = b_x.

Kerroin b_x on siis vektorin b skalaarikomponentti kantavektorin i suunnalle eli x-akselille; lineaariyhdistelyn termi b_xi on vastaavasti vektorikomponentti. Vastaava pätee luonnollisesti muillekin kantavektoreille.

vektori  kosini  yksikkövektori  lineaariyhdistely  kantavektori

Kivelä, niinkuin matematiikka, versio 1.12