Sisällön pääryhmät Yhtälöt ja epäyhtälöt Yhtälöryhmät [ 1 2 3 4 5 6 ] ESITIEDOT:  yhtälöt KATSO MYÖS:

Kansisivu  Sisältö  Hakemisto

Yhtälöryhmässä on useita yhtälöitä ja yleensä myös useita tuntemattomia. Tavoitteena on löytää tuntemattomille sellaiset arvot, että kaikki yhtälöt toteutuvat samanaikaisesti. Useimmiten tuntemattomia on yhtä paljon kuin yhtälöitä. Välttämätöntä tämä ei kuitenkaan ole.

Ryhmälle voidaan etsiä ratkaisuja erilaisista lukujoukoista: reaalisia ratkaisuja, kaikkia kompleksisia ratkaisuja tai ratkaisuja jostakin rajoitetummasta lukujoukosta. Vrt. yhtälöön.

Esimerkkejä yhtälöryhmistä ovat seuraavat, missä tuntemattomia on merkitty x, y, z:

a)  ;	b)  ;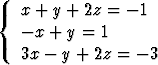
c)  ;	d)  .

Kohdan a yhtälöryhmällä on yksi ainoa ratkaisu, x = 7, y = 1.

Kohdassa b ratkaisuja on äärettömän monta, mutta mikä tahansa lukukolmikko ei kuitenkaan ole ratkaisu; kysymykseen tulevat muotoa x = -1 - t, y = -t, z = t olevat luvut, missä t voidaan valita vapaasti. Jos etsitään reaalisia ratkaisuja, on luonnollisesti t valittava reaaliseksi; kompleksisten ratkaisujen tapauksessa t voi olla mikä tahansa kompleksiluku. Kohdassa c reaalisia ratkaisuja on kaksi; näiden likiarvot ovat x = -0.808901, y = 0.587945 ja x = 0.553738, y = -0.832691.

Kohdassa d on vain yksi reaalinen ratkaisu huolimatta siitä, että yhtälöitä (ehtoja) on vähemmän kuin tuntemattomia: x = y = z = 1.

Kaksi ensimmäistä esimerkkiä ovat lineaarisia yhtälöryhmiä. Tämä ilmenee siten, että yhtälöt ovat ensimmäisen asteen tuntemattomien suhteen, ts. tuntemattomat esiintyvät vain ensimmäisessä potenssissa eivätkä kerrottuina keskenään. Kolmas ja neljäs esimerkki ovat epälineaarisia yhtälöryhmiä.

yhtälö  kompleksiluku  asteluku  polynomi  potenssi (kokonaisluku-)

Kivelä, niinkuin matematiikka, versio 1.12