[#] Sisällön pääryhmät --> Käyrät ja pinnat --> Toisen asteen käyrät [ 1 2 3 4 5 6 7 ]
ESITIEDOT: [#] käyrä, [#] kartio ja lieriö
KATSO MYÖS: [#] ympyrä, [#] toisen asteen pinnat
[#] Kansisivu
[#] Sisältö
[#] Hakemisto

Kartioleikkausten napakoordinaattiyhtälöt

Jos (toinen) polttopiste sijoitetaan origoon, voidaan ellipsi, paraabeli ja hyperbeli esittää napakoordinaattiyhtälön avulla:

r = -----p----- 1 - ecos f,

missä p on vakio ja e eksentrisyys (vakio).

Jos e < 1, kyseessä on ellipsi. Jos e > 1, saadaan hyperbelin toinen haara. Arvo e = 1 antaa paraabelin.

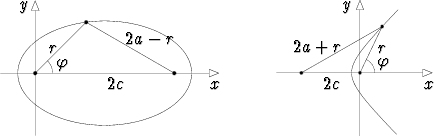
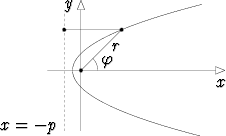
Tässä muodossa on luontevaa käsitellä kartioleikkausten tärkeää sovellusta, planeettaliikettä. Gravitaatiolaista seuraa nimittäin, että jos tarkastellaan yhden planeetan liikettä Auringon ympärillä ottamatta huomioon muiden planeettojen aiheuttamia häiriöitä, rata on ellipsi, paraabeli tai hyperbeli, jonka polttopisteessä Aurinko on.

  [#] koordinaatisto (napa-)

Kivelä, M niinkuin matematiikka, versio 1.12