Sisällön pääryhmät Käyrät ja pinnat Toisen asteen käyrät [ 1 2 3 4 5 6 7 ] ESITIEDOT:  käyrä,  kartio ja lieriö KATSO MYÖS:  ympyrä,  toisen asteen pinnat

Kansisivu  Sisältö  Hakemisto

Ellipsejä, paraabeleja ja hyperbelejä kutsutaan usein yhteisellä nimellä kartioleikkaukset. Tämä johtuu siitä, että suoran ympyräkartion ja tason leikkauskäyrä on aina jokin näistä. Mikä on kyseessä, riippuu leikkaavan tason ja kartion sivuviivan välisestä kulmasta seuraavan kuvion osoittamalla tavalla:

Jos kartion sivuviivan kaltevuuskulma kartion pohjatasoon nähden on ja leikkaavan tason kaltevuuskulma , niin leikkauskäyrä on

ellipsi,	jos < ;
paraabeli,	jos = ;
hyperbeli,	jos > .

Jotta hyperbelin molemmat haarat tulisivat mukaan, on tarkasteltava kartiota kaksihaaraisena, so. kärkipisteensä suhteen symmetrisenä molempiin vastakkaisiin suuntiin avautuvana pintana.

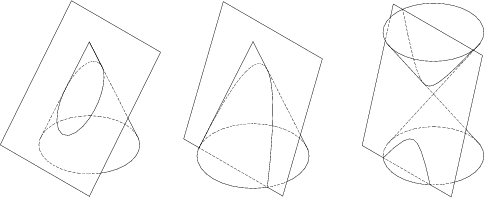
Että leikkauskäyrät todella ovat ellipsejä, paraabeleja ja hyperbelejä, voidaan todistaa synteettisen avaruusgeometrian keinoin. Tällöin on apukonstruktiona sijoitettava kartion sisään kaksi Dandelinin palloa, paraabelitapauksessa yksi. Nämä ovat palloja, jotka sivuavat kartiopintaa pitkin ympyräviivaa ja koskettavat leikkaavaa tasoa yhdessä pisteessä, joka osoittautuu leikkauskäyrän polttopisteeksi.

ympyräkartio (suora)  taso  geometria (synteettinen)  pallo

Kivelä, niinkuin matematiikka, versio 1.12