Ellipsi

Sisällön pääryhmät -->

Käyrät ja pinnat -->

Toisen asteen käyrät [ 1 2 3 4 5 6 7 ]
ESITIEDOT: [#]

käyrä,

kartio ja lieriö
KATSO MYÖS: [#]

ympyrä,

toisen asteen pinnat

Kansisivu

Sisältö

Hakemisto

Ellipsi

Ellipsi voidaan määritellä käyränä, jonka pisteillä on seuraava ominaisuus: Niiden kahdesta kiinteästä pisteestä (polttopisteistä) mitattujen etäisyyksien summa on vakio.

Jos polttopisteiksi valitaan xy-tason pisteet (c, 0) ja (-c, 0) (c > 0) ja em. vakioksi 2a (a > c), saadaan ellipsin yhtälö yksinkertaiseen muotoon:

2
x--
a2 + 2
y--
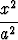b2 = 1,

missä b = V~ a2---c2 . Lukua a sanotaan ellipsin ison akselin puolikkaaksi, luku b on pikku akselin puolikas.

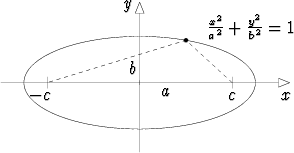
Suhdetta e = c/a kutsutaan ellipsin eksentrisyydeksi ja se mittaa ellipsin litistyneisyyttä. Koska 0 < c < a, on 0 < e < 1.

Jos c = 0, polttopisteet yhtyvät ja käyrästä tulee ympyrä. Eksentrisyys on tällöin e = 0. Jos a on kiinteä ja c --> a, jolloin b --> 0 ja e --> 1, niin ellipsin iso akseli säilyy muuttumattomana, mutta pikku akseli pienenee ja käyrä litistyy kohden polttopisteitä yhdistävää janaa.

Nimitys polttopiste aiheutuu siitä, että jos toisesta polttopisteestä lähtee säde, joka ellipsiin osuessaan heijastuu heijastumislain mukaisesti, niin heijastunut säde kulkee toisen polttopisteen kautta. Geometrisesti tulkittuna tämä tarkoittaa, että ellipsin pisteestä polttopisteisiin piirrettyjen janojen välisen kulman puolittaja on ellipsin normaali. Ellipsille käytetään usein myös parametriesitystä: x = a cos t, y = b sin t, t [0, 2].