[#] Sisällön pääryhmät --> Käyrät ja pinnat --> Toisen asteen käyrät [ 1 2 3 4 5 6 7 ]
ESITIEDOT: [#] käyrä, [#] kartio ja lieriö
KATSO MYÖS: [#] ympyrä, [#] toisen asteen pinnat
[#] Kansisivu
[#] Sisältö
[#] Hakemisto

Liittohyperbeli ja asymptootit

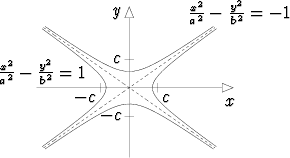
Jos hyperbelinyhtälössä

2 x-- a2 - 2 y-- b2 = 1,

koordinaattien x ja y roolit vaihdetaan, jolloin hyperbelin polttopisteet (0, c) ja (0, -c) sijoitetaan y-akselille, ja vakioksi otetaan 2b, saadaan alkuperäisen hyperbelin liittohyperbeli

2 x-- a2 - 2 y-- b2 = -1.

Jos yhtälössä asetetaan oikeaksi puoleksi 0, saadaan toisen asteen yhtälö, joka esittää kahta suoraa:

2 x-- a2 - 2 y-- b2 = 0 eli y = ±b- a x.

Näitä kutsutaan hyperbelin ja liittohyperbelin yhteisiksi asymptooteiksi.

  [#] asymptootti (rationaalifunktion)
 [#] asymptootti (hyperbelin)

Kivelä, M niinkuin matematiikka, versio 1.12