Sisällön pääryhmät Käyrät ja pinnat Toisen asteen käyrät [ 1 2 3 4 5 6 7 ] ESITIEDOT:  käyrä,  kartio ja lieriö KATSO MYÖS:  ympyrä,  toisen asteen pinnat

Kansisivu  Sisältö  Hakemisto

Hyperbeli määritellään samaan tapaan kuin ellipsi. Kyseessä on käyrä, jonka pisteillä on seuraava ominaisuus: Niiden kahdesta kiinteästä pisteestä (polttopisteistä) mitattujen etäisyyksien erotuksen itseisarvo on vakio.

Kun polttopisteiksi valitaan xy-tason pisteet (c, 0) ja (-c, 0) (c > 0) ja vakioksi 2a (0 < a < c), saadaan hyperbelille yhtälö

- = 1,

missä b = . Lukuja a ja b sanotaan hyperbelin puoliakseleiksi.

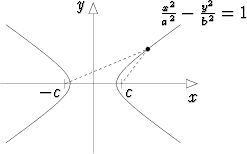
Jos a = b, sanotaan, että hyperbeli on tasasivuinen.

Suhde e = c/a on hyperbelin eksentrisyys. Koska c > a, on e > 1.

Hyperbelillä on monia samantyyppisiä geometrisia ominaisuuksia kuin ellipsillä. Esimerkiksi hyperbelin pisteestä polttopisteisiin piirrettyjen yhdysjanojen välisen kulman puolittaja on hyperbelin tangentti. Hyperbelille voidaan käyttää parametriesitystä x = ±a cosh t, y = b sinh t, t .

käyrä (taso-)  koordinaatisto (xy-)  yhtälö  tangentti (suora)  parametriesitys (tasokäyrän)  hyperbelisini  hyperbelikosini

Kivelä, niinkuin matematiikka, versio 1.12