Sisällön pääryhmät Käyrät ja pinnat Toisen asteen pinnat [ 1 2 3 4 5 ] ESITIEDOT:  pinta KATSO MYÖS:  toisen asteen käyrät,  pallo,  kartio ja lieriö

Kansisivu  Sisältö  Hakemisto

Muotoa

+ - = d

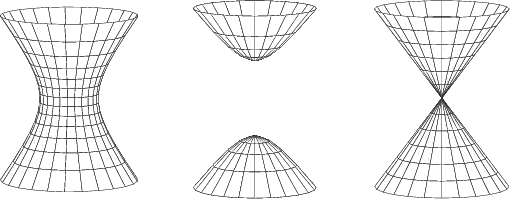
oleva toisen asteen yhtälö, missä a, b ja c ovat mitä tahansa nollasta eroavia vakioita ja d = 1, -1 tai 0, esittää hyperboloidityypin pintaa. Jos d = 1, kyseessä on yksivaippainen hyperboloidi; jos d = -1, pinta on kaksivaippainen hyperboloidi. Jos d = 0, kyseessä on näiden väliin jäävä kartiopinta, jota kutsutaan myös hyperboloidien asymptoottikartioksi.

Jos kartiotapauksessa a = b, saadaan suora ympyräkartio, ts. pinnan poikkileikkaus akselia vastaan kohtisuoralla tasolla on ympyrä.

yhtälö  koordinaatisto (xyz-)  hyperbeli  kartiopinta  kartiopinta  ympyräkartio (suora)

Kivelä, niinkuin matematiikka, versio 1.12