Sisällön pääryhmät Käyrät ja pinnat Toisen asteen pinnat [ 1 2 3 4 5 ] ESITIEDOT:  pinta KATSO MYÖS:  toisen asteen käyrät,  pallo,  kartio ja lieriö

Kansisivu  Sisältö  Hakemisto

Toista astetta olevien lieriöpintojen perustyypit ovat elliptinen lieriö, parabolinen lieriö ja hyperbolinen lieriö, joiden yhtälöt ovat

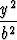+ = 1,   - = 1,   y = ax².

Jos elliptisessä lieriössä on a = b, saadaan suora ympyrälieriö, jonka poikkileikkaus akselia vastaan kohtisuoralla tasolla on ympyrä.

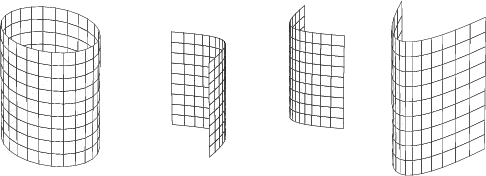
Eo. yhtälöt ovat samoja kuin xy-tason ellipsin, hyperbelin ja paraabelin yhtälöt. Koska ne eivät lainkaan sisällä muuttujaa z, niiden tulkitseminen kolmiulotteisen avaruuden pinnoiksi merkitsee, että jos piste (x, y, 0) on kyseisellä xy-tason käyrällä, niin piste (x, y, z) on pinnalla z-arvosta riippumatta. Pinnat ovat siis lieriöpintoja, jotka syntyvät siten, että pystysuorassa asennossa liikkuva suora tukeutuu kyseiseen xy-tason käyrään.

lieriöpinta  lieriöpinta  yhtälö  koordinaatisto (xyz-)  ympyrälieriö (suora)  ellipsi  hyperbeli  paraabeli

Kivelä, niinkuin matematiikka, versio 1.12