Sisällön pääryhmät Tangentti ja normaali, geometriset kuvaukset Geometriset kuvaukset [ 1 2 3 4 5 6 7 ] ESITIEDOT:  funktiokäsite,  piste,  koordinaatistot KATSO MYÖS:  tangentti ja normaali,  kompleksiluvut

Kansisivu  Sisältö  Hakemisto

Geometriseksi kuvaukseksi kutsutaan funktiota, jonka lähtöjoukkona ja samoin maalijoukkona on tasogeometriassa koko taso ja avaruusgeometriassa koko kolmiulotteinen avaruus.

Kuvaus liittää jokaiseen lähtöjoukon pisteeseen P jonkin maalijoukon pisteen P '. Merkitään P ' = F (P ), missä F on kuvauksen nimi.

Kuvaus F voidaan ilmoittaa kertomalla, miten kuvapisteen P ' suorakulmaiset koordinaatit (x', y') lasketaan, kun argumenttipisteen P koordinaatit (x, y) tiedetään; avaruudessa vastaavasti (x', y', z') ja (x, y, z):

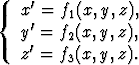
Geometrisen kuvion kuvautuminen määritetään periaatteessa pisteittäin: lasketaan kuvion jokaisen pisteen kuva erikseen.

Tasotapauksessa kuvaus voidaan esimerkiksi määritellä yhtälöillä

Tässä jokainen suora kuvautuu suoraksi ja esimerkiksi ympyrän kuva on ellipsi:

Kuvaukset voivat olla monimutkaisempiakin eikä suoran välttämättä tarvitse kuvautua suoraksi, vaan tuloksena voi aivan hyvin olla jokin käyrä.

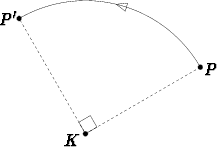
Kuvaus voidaan toisaalta määritellä myös synteettisen geometrian käsittein. Esimerkiksi pisteen P kuvaksi asetetaan piste, joka saadaan kiertämällä tätä 90^o positiiviseen suuntaan pitkin ympyräviivaa, jonka keskipisteenä on kiinteä piste K.

funktio  kuvaus  lähtöjoukko  maalijoukko  suora  ympyrä  ellipsi  geometria (synteettinen)

Kivelä, niinkuin matematiikka, versio 1.12