Sisällön pääryhmät Tangentti ja normaali, geometriset kuvaukset Tangentti ja normaali [ 1 2 3 4 ] ESITIEDOT:  suora,  käyrä,  pinta KATSO MYÖS:  geometriset probleemat,  geometriset kuvaukset

Kansisivu  Sisältö  Hakemisto

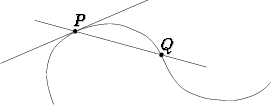
Suoraa, joka leikkaa tarkasteltavaa käyrää vähintään kahdessa pisteessä, kutsutaan käyrän sekantiksi.

Olkoon leikkauspiste P kiinteä ja lähestyköön toinen leikkauspiste Q sitä käyrää pitkin. Jos käyrä on sileä pisteen P kohdalla, ts. kyseessä ei ole käyrällä oleva kärkipiste tai muulla tavoin epäsäännöllinen piste, kääntyy sekantti tällöin suoraksi, joka sivuaa käyrää pisteessä P . Siitä tulee tällöin käyrän tangentti eli sivuaja.

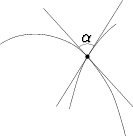
Muodossa y = f(x) annetun tasokäyrän tangentin yhtälö voidaan määrittää derivaatan avulla. Sama koskee minkä tahansa käyrän tangenttisuunnan määrittämistä vektorina. Kahden käyrän sanotaan leikkaavan toisensa kulmassa , jos käyrien leikkauspisteeseen asetettujen tangenttien välinen kulma on .

suora  käyrä (taso-)  käyrä (avaruus-)  derivaatta  differentiaali  tangenttivektori  kulma (taso-)

Kivelä, niinkuin matematiikka, versio 1.12