Sisällön pääryhmät Todennäköisyys Tilastomatematiikka [ 1 2 3 4 5 6 7 8 ] ESITIEDOT: KATSO MYÖS:  todennäköisyyslaskenta,  todennäköisyysjakaumat,  keskiarvo

Kansisivu  Sisältö  Hakemisto

Matemaattisen tilastotieteen perusprobleema on tutkittavaan ilmiöön liittyvän todennäköisyysjakauman tunnuslukujen määrittäminen.

Olkoon tarkasteltavana ilmiö, jonka oletetaan luonteensa perusteella noudattavan jotakin todennäköisyysjakaumaa, mutta jotkin jakauman parametrit — esimerkiksi tiheysfunktion lausekkeessa olevat vakiot — ovat tuntemattomia. Näiden määrittämiseksi voidaan muodostaa otos, jonka avulla pyritään arvioimaan eli estimoimaan parametreille sopivat arvot.

Esimerkiksi voidaan olettaa, että ihmisten pituudet noudattavat normaalijakaumaa, mutta tämän odotusarvo 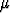ja keskihajonta ovat tuntemattomia. Mittaamalla sopivasti valittu ihmisjoukko (otos), voidaan nämä estimoida.

Jos otosdataa merkitään x₁, x₂, ..., x_n, saadaan todennäköisyyslaskennan teorian perusteella odotusarvon estimaatiksi (jakaumasta riippumatta) otoskeskiarvo

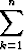= x_k (= ).

Keskihajonnan estimaatti on vastaavasti otoskeskihajonta

= .

Tämä poikkeaa koko datan keskihajonnasta s siten, että summamerkin edessä on jakajana n - 1 havaintojen lukumäärän n sijasta.

Tuntemattomat parametrit voivat olla muunkinlaisia. Niiden estimaateille johdetaan vastaavantyyppiset lausekkeet todennäköisyyslaskennan teorian avulla.

tiheysfunktio  jakauma (normaali-)  odotusarvo  keskihajonta  keskihajonta  todennäköisyyslaskenta  summamerkintä

Kivelä, niinkuin matematiikka, versio 1.12