Sisällön pääryhmät Derivaatta Derivaatta [ 1 2 3 4 5 6 ] ESITIEDOT:  reaalifunktiot,  funktion raja-arvo KATSO MYÖS:  derivointisäännöt,  alkeisfunktioiden derivaatat

Kansisivu  Sisältö  Hakemisto

Määritellään kahden muuttujan funktio (x, h) asettamalla

(x, h) = 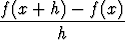- f'(x).

Koska derivoituvalla funktiolla erotusosamäärän raja-arvo on derivaatta, on

lim_h0(x, h) = 0.

Kertomalla eo. yhtälö symbolilla h ja siirtämällä termejä yhtäläisyysmerkin puolelta toiselle, saadaan

f(x + h) - f(x) = f'(x)h + h(x, h),

missä funktion lisäys f(x + h) - f(x) välillä [x,  x + h] on hajotettu kahdeksi termiksi: Edellinen termi

df = f'(x)h

on funktion differentiaali, jälkimmäistä h(x, h) (missä lim_h0(x, h) = 0) kutsutaan yleensä korjaustermiksi. Differentiaalin sanotaan edustavan funktion f lisäyksen lineaarista (suoraviivaista) osaa. Funktion lisäyksen hajottamista tällä tavoin kutsutaan funktion differentiaalikehitelmäksi.

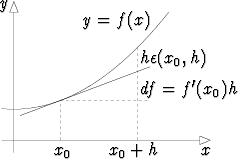
Tekemällä differentiaalikehitelmässä korvaukset x x₀, x + h x, h x - x₀ se voidaan kirjoittaa muotoon

y = f(x) = f(x₀) + f'(x₀)(x - x₀) + (x - x₀)(x₀, x - x₀).

Korjaustermin pois jättäminen voidaan tämän perusteella luonnehtia siten, että käyrä y = f(x) tulee korvatuksi tangentilla y = f(x₀) + f'(x₀)(x - x₀).

Differentiaalikehitelmästä nähdään myös, että derivoituva funktio on aina myös jatkuva:

lim_xx0f(x) = lim_xx0[f(x₀)+f'(x₀)(x-x₀)+(x-x₀)(x₀, x-x₀)] = f(x₀).

funktio (kahden muuttujan)  raja-arvo (funktion)  väli (reaaliakselin)  käyrä (taso-)  tangentti (suora)  jatkuvuus

Kivelä, niinkuin matematiikka, versio 1.12