Sisällön pääryhmät Yhtälöt ja epäyhtälöt Epäyhtälöt [ 1 2 3 4 5 6 7 ] ESITIEDOT:  yhtälöt KATSO MYÖS:

Kansisivu  Sisältö  Hakemisto

Trigonometrinen epäyhtälö

cos²x - sin²x > 0

voidaan ratkaista kahdellakin tavalla.

Vasen puoli voidaan hajottaa kahden tekijän tuloksi, jolloin saadaan (cos x + sin x)(cos x - sin x). Tekijöiden merkkien tutkimiseksi on ensin ratkaistava trigonometriset yhtälöt cos x + sin x = 0 ja cos x - sin x = 0. Trigonometrian kaavojen perusteella nämä saadaan muotoon cos x = cos( + x) ja cos x = cos( - x), joista seuraa nollakohdiksi x = ±/4 + n, missä n on kokonaisluku. Tutkimalla kummankin tekijän merkit alueella [-, ], saadaan seuraava kuvio:

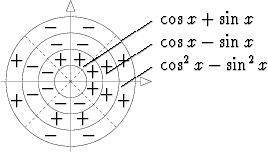
Ottamalla lisäksi huomioon sini- ja kosinifunktioiden jaksollisuus (jaksona 2) saadaan epäyhtälön ratkaisuksi -/4 + n < x < /4 + n, n .

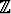Toisena vaihtoehtona on kirjoittaa epäyhtälön vasen puoli kaksinkertaisen kulman kosinin kaavan avulla uuteen muotoon: cos 2x > 0. Tällöin tulee olla -/2 + 2n < 2x < /2 + 2n, mistä kakkosella jakamalla päästään samaan ratkaisuun kuin edellä.

Kumpaa tahansa tapaa käytettäessä on funktioiden kuvaajien piirtämisestä suurta apua.

tekijöihin jako (polynomin)  tekijöihin jako (polynomin)  tekijöihin jako (polynomin)  yhtälö (trigonometrinen)  trigonometria (peruskaavat)  väli (reaaliakselin)  sini  kosini  jaksollinen (funktio)  kuvaaja

Kivelä, niinkuin matematiikka, versio 1.12