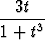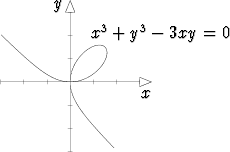Parametriesityksen muodostaminen
Muodossa y = f(x) tai r = f( ) annetut käyrät voidaan parametrisoida helposti:
Jos parametriksi otetaan x tai
) annetut käyrät voidaan parametrisoida helposti:
Jos parametriksi otetaan x tai  , esitykset ovat
, esitykset ovat
r(x) = x i + f(x) j, r( ) = f(
) = f( ) cos
) cos  i + f(
i + f( ) sin
) sin  j.
j.
Jos käyrä on annettu muodossa F (x, y) = 0, ei parametrisointi välttämättä ole
helppoa. Parametriksi on usein syytä valita muuttuja, jolla on jokin luonnollinen
geometrinen merkitys.
Ympyrän x2 + y2 = 4 parametriesityksessä x = 2 cos t, y = 2 sin t parametri
t on ympyrän pistettä (x, y) vastaava keskuskulma. Cartesiuksen lehti
x3 + y3 - 3xy = 0 voidaan parametrisoida ottamalla parametriksi origon
kautta kulkevan suoran y = tx kulmakerroin t, jolloin parametriesitykseksi
saadaan
x = 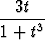 , y =
, y =  .
.
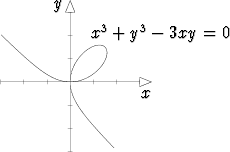
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Käyrät ja pinnat
Käyrät ja pinnat  Käyrä [ 1 2 3 4
]
Käyrä [ 1 2 3 4
]
![[#]](kuvat/msam10-c-4.gif) funktiokäsite,
funktiokäsite, ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) yhtälöt,
yhtälöt, ![[#]](kuvat/msam10-c-4.gif) koordinaatistot,
koordinaatistot,
![[#]](kuvat/msam10-c-4.gif) piste
piste
![[#]](kuvat/msam10-c-4.gif) suora,
suora, ![[#]](kuvat/msam10-c-4.gif) derivaatta,
derivaatta, ![[#]](kuvat/msam10-c-4.gif) tangentti ja normaali,
tangentti ja normaali, ![[#]](kuvat/msam10-c-4.gif) pinta
pinta
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto