Sisällön pääryhmät Geometrian peruskäsitteet Suora [ 1 2 3 4 5 ] ESITIEDOT:  vektori,  koordinaatistot,  piste KATSO MYÖS:  geometria,  vektorialgebra,  geometriset probleemat,  taso

Kansisivu  Sisältö  Hakemisto

Olkoon tasossa piste P₀  r₀ suoran s piste ja olkoon n suoraa vastaan kohtisuora vektori, ns. normaalivektori.

Jotta piste P   r olisi suoralla, on vektoreiden n ja r - r₀ ilmeisestikin oltava toisiaan vastaan kohtisuorat, ts. niiden skalaaritulon n ^. (r - r₀) on oltava = 0.

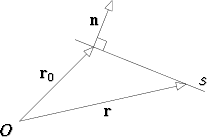
Kun merkitään  r = x i + y j,  r₀ = x₀ i + y₀ j,  n = a i + b j,  saa ehto muodon

n ^. (r - r₀) = a(x - x₀) + b(y - y₀) = 0

eli

ax + by + c = 0,

missä on merkitty c = -ax₀ - by₀. Tätä sanotaan suoran yhtälöksi xy-koordinaatistossa. Huomattakoon, että koordinaattien x ja y kertoimina ovat normaalivektorin komponentit. Piste (x, y) on siis suoralla, jos ja vain jos ehto ax + by + c = 0 toteutuu.

Kolmiulotteisessa euklidisessa avaruudessa ei vastaavalla tavalla voida muodostaa yhtälöä suoralle, vaan analoginen tarkastelu johtaa tason yhtälöön. Suoraa voidaan tällöin käsitellä kahden tason leikkauskuviona, jolloin se esitetään kahdella tason yhtälöllä.

Yhtälöiden käyttö suorien esittämiseen johtaa ns. analyyttiseen geometriaan, jossa geometrisia ongelmia ratkaistaan algebran menetelmillä.

vektori  skalaaritulo  koordinaatisto (xy-)  komponentti  taso (yhtälö)  geometria (analyyttinen)

Kivelä, niinkuin matematiikka, versio 1.12