Sini- ja kosinilauseen todistamisesta
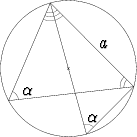
Sinilauseen ensimmäinen osa sin  = a/(2r) voidaan todistaa muodostamalla
kolmion ympäri piirretyn ympyrän sisään uusi kolmio, jonka yhtenä sivuna on
alkuperäisen kolmion sivu a ja toisena ympyrän halkaisija. Halkaisijan vastainen
kulma (ympyrän kehäkulma) on suora, kuten esimerkiksi vektorigeometrialla
nähdään. Tulos seuraa tämän jälkeen sinin määritelmästä (vastainen kateetti /
hypotenuusa) ja siitä, että ympyrässä kaikki samaa kaarta vastaavat kehäkulmat
ovat yhtä suuria.
= a/(2r) voidaan todistaa muodostamalla
kolmion ympäri piirretyn ympyrän sisään uusi kolmio, jonka yhtenä sivuna on
alkuperäisen kolmion sivu a ja toisena ympyrän halkaisija. Halkaisijan vastainen
kulma (ympyrän kehäkulma) on suora, kuten esimerkiksi vektorigeometrialla
nähdään. Tulos seuraa tämän jälkeen sinin määritelmästä (vastainen kateetti /
hypotenuusa) ja siitä, että ympyrässä kaikki samaa kaarta vastaavat kehäkulmat
ovat yhtä suuria.
Kosinilauseen todistaminen on yksinkertainen vektorigeometrian sovellus: Jos
kolmion sivuvektorit ovat a ja b, on kolmannen sivun vektoriesitys a - b. Tällöin
on skalaaritulon ominaisuuksien perusteella
c2 = (a - b) . (a - b) = a . a + b . b - 2a . b = a2 + b2 - 2ab cos 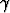 .
.
Kosinilause on itse asiassa Pythagoraan lauseen yleistys: Jos 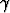 = 90o, saadaan
Pythagoraan lause.
= 90o, saadaan
Pythagoraan lause.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Kulma, kolmio, monikulmio ja -tahokas
Kulma, kolmio, monikulmio ja -tahokas  Kolmio [ 1 2 3 4 5 6 7 8 9 10 11 ]
Kolmio [ 1 2 3 4 5 6 7 8 9 10 11 ]
![[#]](kuvat/msam10-c-4.gif) piste,
piste, ![[#]](kuvat/msam10-c-4.gif) suora,
suora, ![[#]](kuvat/msam10-c-4.gif) kulma
kulma
![[#]](kuvat/msam10-c-4.gif) geometriset probleemat,
geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) Pythagoraan lause,
Pythagoraan lause, ![[#]](kuvat/msam10-c-4.gif) monikulmiot
monikulmiot
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto

 .
.