![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Lukujonon ja funktion raja-arvo
Lukujonon ja funktion raja-arvo  Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ]
Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) lukujonot
lukujonot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) funktion raja-arvo,
funktion raja-arvo, ![[#]](kuvat/msam10-c-4.gif) Neperin luku e
Neperin luku e
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Lukujonon ja funktion raja-arvo Lukujonon ja funktion raja-arvo  Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ] Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) lukujonot lukujonot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) funktion raja-arvo, funktion raja-arvo, ![[#]](kuvat/msam10-c-4.gif) Neperin luku e Neperin luku e
|
|
Raja-arvojen laskeminen pohjautuu määritelmän perusteella ’itsestään selviin’ tuloksiin sekä summan, erotuksen, tulon ja osamäärän raja-arvoa koskeviin lauseisiin. Lisäksi on syytä tuntea eräitä ’standardiraja-arvoja’ (käsittely edempänä), jotka voidaan perustella suoraan määritelmän avulla, vaikkakaan ei aivan yksinkertaisesti.
Itsestään selviä, oikeastaan suoraan määritelmiin palautuvia tuloksia ovat ennen muuta
limn

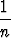 = 0 ja limn
= 0 ja limn
 n =
n = 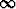 .
.
Tietty varovaisuus ’itsestään selvyydessä’ on kuitenkin paikallaan. Erityisesti on
huomattava, että jos lauseke näyttäisi rajaprosessissa saavan muodon 0/0, 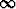 /
/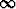 ,
0 .
,
0 . 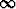 ,
, 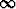 -
- 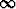 tai 1
tai 1 , sen raja-arvosta ei tämän perusteella voida päätellä
mitään. Varsinkin viimeiseksi mainittu on syytä huomata: Esimerkiksi
Neperin luku e = 2.718... saadaan raja-arvona limn
, sen raja-arvosta ei tämän perusteella voida päätellä
mitään. Varsinkin viimeiseksi mainittu on syytä huomata: Esimerkiksi
Neperin luku e = 2.718... saadaan raja-arvona limn
 (1 + 1/n)n, mikä
muodollisesti laskien antaa 1
(1 + 1/n)n, mikä
muodollisesti laskien antaa 1 ja siis johtaa kiusaukseen päätellä raja-arvoksi
1.
ja siis johtaa kiusaukseen päätellä raja-arvoksi
1.
Raja-arvon laskemisen suhtautuminen laskutoimituksiin ilmenee seuraavista
kaavoista, joissa oletetaan, että raja-arvot limn
 an ja limn
an ja limn
 bn ovat
olemassa:
bn ovat
olemassa:
limn  (an ± bn) = limn (an ± bn) = limn  an ± limn an ± limn  bn; bn; |
limn  (can) = c limn (can) = c limn  an (c vakio); an (c vakio); |
limn  (anbn) = limn (anbn) = limn  an . limn an . limn  bn; bn; |
limn   = =  . . |
Osamäärää koskevassa kaavassa tulee luonnollisesti nimittäjien olla  0.
0.
![[#]](kuvat/msam10-c-4.gif) raja-arvo (standardi-, lukujonon) raja-arvo (standardi-, lukujonon)![[#]](kuvat/msam10-c-4.gif) Neperin luku Neperin luku |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12