![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Lukujonon ja funktion raja-arvo
Lukujonon ja funktion raja-arvo  Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ]
Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) lukujonot
lukujonot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) funktion raja-arvo,
funktion raja-arvo, ![[#]](kuvat/msam10-c-4.gif) Neperin luku e
Neperin luku e
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Lukujonon ja funktion raja-arvo Lukujonon ja funktion raja-arvo  Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ] Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) lukujonot lukujonot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) funktion raja-arvo, funktion raja-arvo, ![[#]](kuvat/msam10-c-4.gif) Neperin luku e Neperin luku e
|
|
1) Tyypillinen esimerkki eo. kaavojen käytöstä on seuraava lasku, missä on itse
asiassa käytetty jokaista kaavaa ja palautettu näiden avulla raja-arvon
laskeminen yksittäisten termien raja-arvoihin ja lopulta ’itsestään selvyyteen’
limn
 1/n = 0:
1/n = 0:
 =
=  -
- n
n

 .
.
2) Toisinaan on lauseke kirjoitettava sopivaan uuteen muotoon raja-arvon
määrittämiseksi. Koska lauseke  -
-  saa muodon
saa muodon 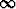 -
- 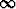 , kun
n
, kun
n 
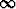 , ei raja-arvosta voida suoraan päätellä mitään. Laventaminen lausekkeella
, ei raja-arvosta voida suoraan päätellä mitään. Laventaminen lausekkeella
 +
+  johtaa kuitenkin tulokseen:
johtaa kuitenkin tulokseen:
 -
-  =
=  =
=  -
- n
n

 .
.
Oikeastaan tässä on myös käytetty neliöjuurifunktion jatkuvuutta. (Missä kohdassa?)
Raja-arvoja voi luonnollisesti tutkia myös laskemalla numeerisesti jonon lukuja. Tällä tavoin voi usein selvittää ainakin sen, mikä luku raja-arvo ei ainakaan ole. Tiettyä varovaisuutta on kuitenkin noudatettava, koska numeerisessa laskennassa aina tapahtuvat pyöristysvirheet voivat aiheuttaa katastrofaalisesti vääriä tuloksia. Ks. esimerkkiä Neperin luvusta edempänä.
![[#]](kuvat/msam10-c-4.gif) laventaminen laventaminen![[#]](kuvat/msam10-c-4.gif) neliöjuurifunktio neliöjuurifunktio![[#]](kuvat/msam10-c-4.gif) jatkuvuus jatkuvuus![[#]](kuvat/msam10-c-4.gif) Neperin luku (numeerisesti) Neperin luku (numeerisesti) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12