Sisällön pääryhmät Tangentti ja normaali, geometriset kuvaukset Tangentti ja normaali [ 1 2 3 4 ] ESITIEDOT:  suora,  käyrä,  pinta KATSO MYÖS:  geometriset probleemat,  geometriset kuvaukset

Kansisivu  Sisältö  Hakemisto

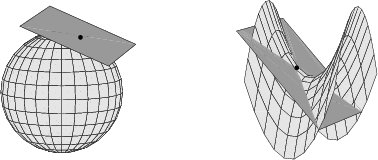
Käyrän tangenttia (suoraa) vastaa pinnan tangenttitaso. Pinnan pisteeseen P asetettu tangenttitaso voidaan määritellä tasoksi, joka sisältää kaikki ne pisteen P kautta kulkevat suorat, jotka ovat tangentteja jollekin pinnalla sijaitsevalle pisteen P kautta kulkevalle käyrälle. Tangenttitason sanotaan sivuavan pintaa pisteessä P .

Jotta pinnalla olisi tangenttitaso tietyssä pisteessä, tulee sen olla sileä tämän pisteen kohdalla. Esimerkiksi kartiolla ei ole tangenttitasoa kärkipisteessä.

Pinnalla ja tangenttitasolla voi sivuamispisteen ympäristössä olla muitakin yhteisiä pisteitä. Esimerkiksi satulapinta leikkaa tangenttitasoaan pitkin kahta sivuamispisteen kautta kulkevaa suoraa.

Muodossa z = f(x, y) annetun pinnan tangenttitaso voidaan määrittää differentiaalilaskennan keinoin; tällöin kuitenkin tarvitaan kahden muuttujan funktion f(x, y) osittaisderivaatan käsitettä.

käyrä (taso-)  käyrä (avaruus-)  suora  pinta  taso  kartio  satulapinta  funktio (kahden muuttujan)

Kivelä, niinkuin matematiikka, versio 1.12