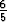Sisällön pääryhmät Geometriset probleemat Vektorigeometriaa [ 1 2 3 ] ESITIEDOT:  vektori,  vektorialgebra,  koordinaatistot,  piste,  suora,  taso KATSO MYÖS:  geometriset probleemat,  kolmio,  kulma,  ympyrä

Kansisivu  Sisältö  Hakemisto

Vesipisara putoaa tasolle x + 2y + 3z = 4 pisteeseen (-3, -1, 3) ja alkaa valua tasoa pitkin. Missä pisteessä se kohtaa xy-tason? Oletetaan tavanomaiseen tapaan, että z-akseli on pystysuora ja osoittaa ylöspäin, jolloin painovoima vaikuttaa negatiivisen z-akselin suuntaan.

Merkitään putoamispisteen paikkavektoria p = -3i - j + 3k.

Tason normaalivektori on n = i + 2j + 3k. Koska z-akselin suuntainen kantavektori k on pystysuora, saadaan ristitulon avulla vaakasuora tason suuntainen vektori s = k × n = -2i + j .

Pisaran valumissuunta on kohtisuorassa tason normaalivektoria vastaan ja toisaalta se on mahdollisimman jyrkkä, jolloin sen tulee olla kohtisuorassa myös edellä muodostettua vektoria s vastaan. Valumissuunta — tai mahdollisesti vastakkainen suunta — sadaan ristitulosta

v = s × n = 3i + 6j - 5k.

Tämä on todellakin valumissuunta, koska k-komponentti on negatiivinen; ristitulo n × s olisi antanut vastakkaisen suunnan.

Paikkavektori, joka osoittaa origosta siihen pisteeseen, missä pisara kohtaa xy-tason, on siis muotoa

p + v = (-3 + 3)i + (-1 + 6)j + (3 - 5)k.

Koska piste sijaitsee xy-tasossa, tulee olla 3 - 5 = 0 eli = . Pisteen x- ja y-koordinaatti ovat tällöin

x = -3 + 3 = -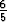, y = -1 + 6 = .

taso (yhtälö)  koordinaatisto (xyz-)  paikkavektori  normaalivektori (tason)  kantavektori  ristitulo  vektoritulo  vektoritulon laskeminen

Kivelä, niinkuin matematiikka, versio 1.12