Esimerkki 1 vektorigeometriasta
Kolmion keskijanojen leikkaaminen samassa pisteessä voidaan helposti todistaa
vektorigeometrian menetelmin.
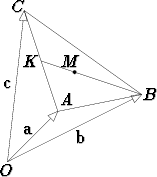
Kolmion kärkipisteet olkoot A, B ja C ja olkoot kiinteästä pisteestä O
näihin pisteisiin osoittavat vektorit a, b ja c (pisteiden paikkavektorit).
Olkoon K janan AC keskipiste ja valitaan piste M keskijanalta BK siten,
että |KM| : |MB| = 1 : 2. Tällöin saadaan seuraavat vektoriesitykset:
Vektorin  esitys on siis symmetrinen vektoreiden a, b, c suhteen, ts. samaan
tulokseen tultaisiin laskemalla vektoriesitys millä tahansa keskijanalla sijaitsevalle
pisteelle, joka jakaa kyseisen janan suhteessa 1 : 2. Tästä seuraa, että näiden
jakopisteiden tulee yhtyä, jolloin väite tulee todistetuksi.
esitys on siis symmetrinen vektoreiden a, b, c suhteen, ts. samaan
tulokseen tultaisiin laskemalla vektoriesitys millä tahansa keskijanalla sijaitsevalle
pisteelle, joka jakaa kyseisen janan suhteessa 1 : 2. Tästä seuraa, että näiden
jakopisteiden tulee yhtyä, jolloin väite tulee todistetuksi.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometriset probleemat
Geometriset probleemat  Vektorigeometriaa
[ 1 2 3 ]
Vektorigeometriaa
[ 1 2 3 ]
![[#]](kuvat/msam10-c-4.gif) vektori,
vektori, ![[#]](kuvat/msam10-c-4.gif) vektorialgebra,
vektorialgebra, ![[#]](kuvat/msam10-c-4.gif) koordinaatistot,
koordinaatistot, ![[#]](kuvat/msam10-c-4.gif) piste,
piste, ![[#]](kuvat/msam10-c-4.gif) suora,
suora,
![[#]](kuvat/msam10-c-4.gif) taso
taso
![[#]](kuvat/msam10-c-4.gif) geometriset probleemat,
geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) kolmio,
kolmio, ![[#]](kuvat/msam10-c-4.gif) kulma,
kulma, ![[#]](kuvat/msam10-c-4.gif) ympyrä
ympyrä
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto











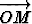







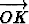

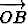

 esitys on siis symmetrinen vektoreiden
esitys on siis symmetrinen vektoreiden 