![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometriset probleemat
Geometriset probleemat  Analyyttista
geometriaa [ 1 2 ]
Analyyttista
geometriaa [ 1 2 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) koordinaatistot,
koordinaatistot, ![[#]](kuvat/msam10-c-4.gif) piste,
piste, ![[#]](kuvat/msam10-c-4.gif) suora,
suora, ![[#]](kuvat/msam10-c-4.gif) taso
taso
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) geometriset probleemat,
geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) ympyrä
ympyrä
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Geometriset probleemat Geometriset probleemat  Analyyttista
geometriaa [ 1 2 ] Analyyttista
geometriaa [ 1 2 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) koordinaatistot, koordinaatistot, ![[#]](kuvat/msam10-c-4.gif) piste, piste, ![[#]](kuvat/msam10-c-4.gif) suora, suora, ![[#]](kuvat/msam10-c-4.gif) taso taso
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) geometriset probleemat, geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) ympyrä ympyrä
|
|
Kolmion kärkipisteet olkoot (x1, y1), (x2, y2) ja (x3, y3). Tavoitteena on analyyttisen geometrian keinoin osoittaa, että kolmion keskijanat leikkaavat toisensa samassa pisteessä.
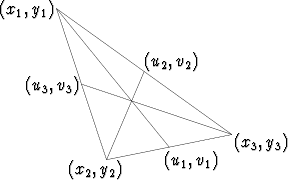
Kolmion sivujen keskipisteiden koordinaatit (u1, v1), (u2, v2) ja (u3, v3) saadaan keskiarvoina kunkin sivun päätepisteiden koordinaateista:
u1 =  (x2 + x3), (x2 + x3), | u2 =  (x3 + x1), (x3 + x1), | u3 =  (x1 + x2), (x1 + x2), |
v1 =  (y2 + y3), (y2 + y3), | v2 = 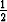 (y3 + y1), (y3 + y1), | v3 = 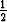 (y1 + y2). (y1 + y2). |
Keskijanasuorien yhtälöt ovat
| y - y1 | = |  (x - x1), (x - x1), | ||
| y - y2 | = |  (x - x2), (x - x2), | ||
| y - y3 | = |  (x - x3). (x - x3). |
| (2x1 - x2 - x3)(y - y1) | = | (2y1 - y2 - y3)(x - x1), | ||
| (2x2 - x3 - x1)(y - y2) | = | (2y2 - y3 - y1)(x - x2), | ||
| (2x3 - x1 - x2)(y - y3) | = | (2y3 - y1 - y2)(x - x3). |
Ratkaisemalla yhtälöryhmä algebrallisesti — mikä vaatii kyllä hieman työntekoa — todetaan, että sillä on yksi ratkaisu:
x =  (x1 + x2 + x3), y =
(x1 + x2 + x3), y =  (y1 + y2 + y3).
(y1 + y2 + y3).
Keskijanat siis leikkaavat toisensa tässä pisteessä.
![[#]](kuvat/msam10-c-4.gif) kolmio kolmio![[#]](kuvat/msam10-c-4.gif) koordinaatisto (xy-) koordinaatisto (xy-)![[#]](kuvat/msam10-c-4.gif) keskijana (esimerkki) keskijana (esimerkki)![[#]](kuvat/msam10-c-4.gif) keskijana (esimerkki) keskijana (esimerkki)![[#]](kuvat/msam10-c-4.gif) keskijana (esimerkki) keskijana (esimerkki)![[#]](kuvat/msam10-c-4.gif) keskijana keskijana![[#]](kuvat/msam10-c-4.gif) suora (yhtälö) suora (yhtälö)![[#]](kuvat/msam10-c-4.gif) kulmakerroin kulmakerroin![[#]](kuvat/msam10-c-4.gif) yhtälöryhmä
(lineaarinen) yhtälöryhmä
(lineaarinen) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12