Sisällön pääryhmät Integraali Määrätty integraali [ 1 2 3 4 5 6 7 8 ] ESITIEDOT:  summa ja tulo,  integraalifunktio KATSO MYÖS:  integroimistekniikkaa

Kansisivu  Sisältö  Hakemisto

Määrätty integraali voidaan laskea integraalifunktion avulla. Jos nimittäin F (x) on jokin funktion f(x) integraalifunktio kaikilla x [a, b], on

f(x) dx = F (b) - F (a).

Tulos tunnetaan analyysin peruslauseen nimellä. Todistusta ei tässä käsitellä.

Usein käytetään merkintöjä

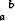F (x) = F (b) - F (a) ja F (x)  = F (b) - F (a).

Esimerkiksi on

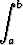ce^-kx dx = - e^-kx = .

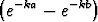Funktion f integraalifunktio voidaan lausua määrätyn integraalin muodossa. Koska f(t) dt = F (x) - F (a), on

f(t) dt = F '(x) = f(x).

Integraalifuntio voidaan siis kirjoittaa muotoon

F (x) = f(t) dt + C.

Huomattakoon, että määrätyn integraalin integroimismuuttuja — edellä t — voi olla mikä tahansa. Sehän katoaa lausekkeesta rajojen sijoittamisen jälkeen.

integraalifunktio  integrointi (kaavat)  integrointi (kaavat)  derivaatta

Kivelä, niinkuin matematiikka, versio 1.12