![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Luvut
Luvut  Reaaliluvut [ 1 2 3 4 5 6 7
]
Reaaliluvut [ 1 2 3 4 5 6 7
]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) murtoluvut,
murtoluvut, ![[#]](kuvat/msam10-c-4.gif) lukujärjestelmät,
lukujärjestelmät, ![[#]](kuvat/msam10-c-4.gif) kompleksiluvut
kompleksiluvut
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Luvut Luvut  Reaaliluvut [ 1 2 3 4 5 6 7
] Reaaliluvut [ 1 2 3 4 5 6 7
]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) murtoluvut, murtoluvut, ![[#]](kuvat/msam10-c-4.gif) lukujärjestelmät, lukujärjestelmät, ![[#]](kuvat/msam10-c-4.gif) kompleksiluvut kompleksiluvut
|
|
Periaatteessa rationaaliluvut riittävät kaikissa käytännöllisissä tehtävissä.
Esimerkiksi minkä tahansa suureen miten tarkka likiarvo tahansa on lausuttavissa
rationaalilukujen avulla: 7.3478 = 7 + 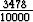 .
.
Teoreettisissa tarkasteluissa rationaaliluvut osoittautuvat riittämättömiksi. Klassisia ongelmia ovat neliön sivun pituuden lausuminen murto-osana lävistäjän pituudesta ja ympyrän kehän pituuden lausuminen halkaisijan avulla. Näistä voidaan todistaa, että verrannollisuuskertoimet eivät ole rationaalilukuja:
Pythagoraan lauseen mukaan neliön sivun pituudelle a ja lävistäjän pituudelle c
pätee c2 = 2a2; alkeellisesti voidaan osoittaa, että rationaalilukua, jonka neliö olisi
2, ei voi olla olemassa. Ympyrän kehän ja halkaisijan pituuksien suhteen — luvun
 — osalta todistus on vaikeampi; sen on ensimmäisenä esittänyt Johann Heinrich
Lambert vuonna 1761.
— osalta todistus on vaikeampi; sen on ensimmäisenä esittänyt Johann Heinrich
Lambert vuonna 1761.
Mainituissa tapauksissakin voitaisiin tietysti tyytyä likiarvoihin, mutta on
miellyttävää ajatella, että on olemassa täsmällinen suhdeluku. Tämä merkitsee
uusien lukujen, irrationaalilukujen liittämistä rationaalilukujen joukkoon.
Rationaaliluvut ja irrationaaliluvut yhdessä muodostavat reaalilukujen joukon,
symbolina  .
.
Irrationaalilukua voitaisiin luonnehtia olioksi, jolle on ainakin periaatteessa mahdollista laskea mielivaltaisen tarkkoja rationaalisia approksimaatioita. Itse asiassa täsmällinen määritelmä voidaan perustaa juuri tähän ajatukseen.
![[#]](kuvat/msam10-c-4.gif) Pythagoraan lause Pythagoraan lause![[#]](kuvat/msam10-c-4.gif) pii pii![[#]](kuvat/msam10-c-4.gif) pii (sarja) pii (sarja)![[#]](kuvat/msam10-c-4.gif) Lambert (pii) Lambert (pii)![[#]](kuvat/msam10-c-4.gif) joukko joukko |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12