[#] Sisällön pääryhmät --> Derivaatta --> Newtonin iteraatio [ 1 2 3 4 ]
ESITIEDOT: [#] yhtälöt, [#] lukujonon raja-arvo, [#] derivaatta
KATSO MYÖS: [#] polynomiyhtälöt, [#] transkendenttiyhtälöt
[#] Kansisivu
[#] Sisältö
[#] Hakemisto

Esimerkki Newtonin iteraatiosta

Esimerkkinä olkoon yhtälön f(x) = x3 - 2x - 5 = 0 avoimella välillä ]2, 3[ olevan juuren etsiminen. Ainakin yksi tällainen on olemassa, sillä f(2) = -1, f(3) = 16 ja funktio f on jatkuva. Newtonin menetelmän iteraatiokaavaksi saadaan

xn+1 = xn - x3 - 2x - 5 -n---2--n---- 3xn - 2.

Jos alkuarvoksi valitaan x0 = 2, antaa iterointi seuraavaa:

x0 = 2
x1 = 2.1
x2 = 2.094568
x3 = 2.09455148170
x4 = 2.09455148154233
x5 = 2.09455148154233
x6 = 2.09455148154233

Lukujono siis näyttää suppenevan. Cardanon kaavojen avulla voidaan tässä tapauksessa saada juurelle myös tarkka arvo:

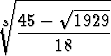x = V~ ------------ V~ ----- 3 45-+---1929- 18 + V~ ------------ V~ ----- 3 45-----1929- 18.

  [#] yhtälö (polynomi-)
 [#] avoin väli
 [#] juuri (yhtälön)
 [#] jatkuvuus
 [#] lukujono
 [#] suppeneminen (lukujonon)
 [#] Cardanon kaavat

Kivelä, M niinkuin matematiikka, versio 1.12