Sisällön pääryhmät Derivaatta Newtonin iteraatio [ 1 2 3 4 ] ESITIEDOT:  yhtälöt,  lukujonon raja-arvo,  derivaatta KATSO MYÖS:  polynomiyhtälöt,  transkendenttiyhtälöt

Kansisivu  Sisältö  Hakemisto

Newtonin menetelmä voidaan johtaa seuraavasti:

Olkoon yhtälöllä f(x) = 0 juurena ja olkoon x₀ tämän approksimaatio, ts. iteraation lähtöarvo. Käyrälle y = f(x) asetetaan tangentti pisteeseen (x₀, f(x₀)). Tämän yhtälö on

y - f(x₀) = f'(x₀)(x - x₀).

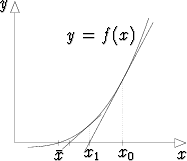
Tangentti leikkaa x-akselin pisteessä, jossa y = 0 ja siis

x = x₁ = x₀ - .

Tämä on kuvion mukaisesti (yleensä) tarkempi approksimaatio juurelle kuin x₀.

Askel toistetaan pitäen saatua arvoa x₁ uutena lähtöarvona, jolloin saadaan jälleen tarkempi approksimaatio x₂. Näin jatketaan ja saadaan muodostetuksi lukujono x₀, x₁, x₂, x₃,  .... Yleisesti laskentaprosessi voidaan esittää iteraatiokaavana:

annettuna x0;

xn+1 = xn - , n = 0, 1, 2, ... .

yhtälö  juuri (yhtälön)  käyrä (taso-)  tangentti (suora)  suora (yhtälö)  derivaatta  differentiaali  lukujono  rekursiivisesti määritelty lukujono

Kivelä, niinkuin matematiikka, versio 1.12